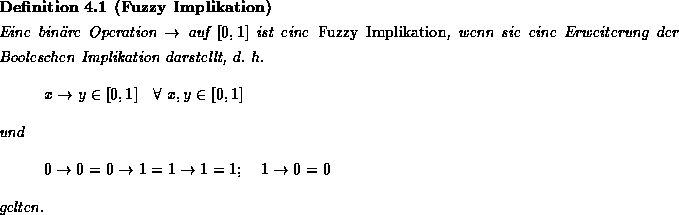
Zur Anwendung von Inferenzregeln benötigen wir eine Erweiterung der Implikation auf Fuzzy Mengen. Fodor und Keresztfalvi [FK93] definieren die Fuzzy Implikation so:
Den Ausführungen des Fuzzy-FAQ [KHJ97] folgend, könnte eine typische Inferenzregel folgendermaßen aussehen: Ist y niedrig und y hoch, dann setze z = mittel
wobei x und y Eingabewerte sind und z ein Ausgabewert ist. Die unscharfen Teilmengen ,, niedrig'' des Wertebereichs von x, ,,hoch'' des Wertebereichs von y, und ,,mittel'' des Wertebereichs von z stellen die Belegungen der linguistischen Variablen dar.
Die Prämisse der Inferenzregel beschreibt den Grad des Zutreffens der Regel, während die Konklusion jedem Ausgabewert einen Zugehörigkeitsgrad zuweist. Der Inferenzmechanismus ermittelt dazu den Wahrheitswert jeder Prämisse (falls mehrere Regeln angewendet werden können, wie dies in Expertensystemen zumeist der Fall ist). Der ermittelte Wahrheitswert wird auf die Konklusion der betreffenden Regel angewendet. Damit wird jeder Ausgabevariablen eine unscharfe Teilmenge zugewiesen. Als Inferenzregeln kommen beispielsweise die oben besprochenen Verfahren Max-Min-Komposition oder Max-Prod-Komposition zum Einsatz.
Fodor und Keresztfalvi [FK93] sehen das Finden geeigneter Verknüpfungen (Konjunktionen, Disjunktionen und Implikationen) als elementares Problem in der Fuzzy Inferenz an. Einen festen Platz haben sich nach ihrer Meinung die t-Normen, die t-Conormen und die starken Negationen geschaffen. Doch oftmals werden diese Operatoren routinemäßig verwendet, obwohl sie eigentlich zu starke Restriktionen beinhalten: Arbeitet man zum Beispiel mit binären Konjunktionen, und besteht keine Notwendigkeit, diese auf drei oder mehr Argumente auszuweiten, wird keine Assoziativität benötigt. Dasselbe gilt für Kommutativität, wenn die beiden Argumente einen unterschiedlichen semantischen Hintergrund haben und nie miteinander vertauscht werden. Daher sahen sich die Autoren veranlaßt, die Definitionen und Eigenschaften von Operatoren in der Fuzzy Logik kritisch zu untersuchen, worauf hier aber nicht näher eingegangen werden kann.
Schefe [Sch81] versucht den Übergang von der klassischen zur Fuzzy Logik, in der für eine atomare Aussage jeder Grad der Zustimmung zugelassen ist, auf eine solide mathematische Basis zu stellen, indem er die Zugehörigkeitswerte als ein mathematisches Maß betrachtet. Er modelliert den Zugehörigkeitsgrad als ein Maß auf Borel-Mengen, die Verknüpfungen als Operatoren auf Borel-Mengen und die logische Inferenz als eine bedingte Zustimmungswahrscheinlichkeit. Dabei setzt er die Wahl alternativer Operatoren für eine Verknüpfung mit der in der Wahrscheinlichkeitstheorie verwendeten Abhängigkeit bzw. Unabhängigkeit von Ereignissen in Beziehung.
Des weiteren bildet er Aussagen nicht auf Zahlen x, sondern auf halboffene Intervalle ]0, x] ab. Diese Intervalle sind meßbar. Die Zustimmungswahrscheinlichkeit ergibt sich dann aus dem Borel-Lebesgue-Maß dieser Intervalle. Die Verknüpfung zweier Intervalle wird durch Vereinigung bzw. Durchschnittsbildung vorgenommen, was bei den hier beschriebenen Intervallen auf Maximum- bzw. Minimumbildung hinausläuft, genau wie im klassischen Fall. Man kann diese Zustimmungswahrscheinlichkeit also als Spezialfall der klassischen Wahrscheinlichkeit betrachten, was den Vorteil hat, daß man sich damit die Theoreme der klassischen Wahrscheinlichkeitstheorie zunutze machen kann.
Ein weiterer großer Vorteil dieser Methode ist die Möglichkeit,
eine
wesentlich geeignetere Negation zu definieren, als dies in der Fuzzy
Mengentheorie möglich ist. Sie wird definiert als 
.
Betrachtet man nun die Tautologie und die Kontradiktion, so erhält
man deren Zutreffenswahrscheinlichkeiten als
,
.
Solche Resultate kann man in der Fuzzy Mengentheorie wegen der mangelhaften Negation nicht erreichen.
Schefe betont, daß das hier vorgestellte Verfahren nicht ,, Wahrheitswerte-funktional'' im klassischen Sinn ist, da man den Wahrheitswert einer zusammengesetzten Aussage nicht auf einheitliche Art und Weise aus den Wahrheitswerten der Teilaussagen ableiten kann, sobald Komplemente in der Aussage enthalten sind. Allerdings erachtet Schefe ein solches System auch nicht für erstrebenswert, da er ein intuitives Verständnis der Tatsache besitzt, daß ,,Wahrheit'' nicht abgestuft werden kann, sondern nur dem klassischen Fall der absoluten Gewißheit zugeordnet werden sollte.
In der klassischen Logik sind Tautologien wie der Modus Ponens 
die Hauptmethoden zur
Schlußfolgerung. Hierbei sind A und B Aussagen, und
die Aussage
B in der Prämisse stimmt mit der Aussage B in der
Konklusion
überein. Zwei offensichtliche Generalisierungen im Sinne der Fuzzy
Logik sind hierbei
Das Resultat, der generalisierte Modus Ponens, ein Inferenzschema mit Fuzzy-Prädikaten, ist also nach Fodor und Keresztfalvi [FK93] gegeben durch
wobei 
und 
Fuzzy-Mengen
des Universums X bzw. Y sind. Diese Fuzzy-Mengen sind
nicht
notwendigerweise normalisiert.
Schefe [Sch81] weist darauf hin, daß bei der Interpretation dieser Aussagen mit Vorsicht zu Werke gegangen werden muß, da es sich um subjektive Gewißheitsaussagen und nicht um Wahrscheinlichkeiten handelt. Ein Zustimmungsgrad wird der gesamten Aussage zugewiesen, nicht der Vermutung selbst. Ein Beispiel ist die Aussage
Es ist zu einem Grad von 0.6 sicher, daß die Vermutung richtig ist.Die Verneinung dieser Aussage muß also lauten
Es ist zu einem Grad von 0.4 nicht sicher, daß die Vermutung richtig ist.und nicht:
Es ist zu einem Grad von 0.4 sicher, daß die Vermutung nicht richtig ist.
Zur Auflösung dieser unscharfen Inferenz schlug Zadeh [Zad73] die Kompositionsregel der Inferenz vor, die nach der Methode des approximativen Schließens verfährt und damit an unser ,, Alltagsdenken'' angelehnt ist:
Verwendet man die Max-M-Komposition, so berechnet sich
folgendermaßen [FK93]:
M ist hierbei eine Fuzzy-Konjunktion. 
ist eine
unscharfe binäre Relation (üblicherweise eine
Implikation) auf 
und beschreibt die
Beziehung zwischen
den Ein- und den Ausgaben.
Zimmermann [Zim91] sieht unscharfe Algorithmen, also Befehlsfolgen, in denen einige Befehle Fuzzy Mengen enthalten, sowie unscharfe Flußdiagramme als die Hauptanwendungsgebiete des unscharfen Schlußfolgerns an.
Mizumoto [Miz84] vergleicht die
Inferenzresultate der
Max-Min-Komposition und der Max-
-Komposition.
Hierbei repräsentiert das
drastische Produkt, das definiert ist als
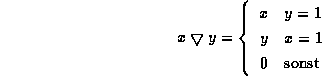
Als Eingabe für die Kompositionsregel der
Inferenz verwendet er eine unscharfe Menge 
, die jeweils
durch eine Vielzahl von Hedges modifiziert wird.
Daneben kommen eine ganze Reihe von Implikationen zum Einsatz (vgl.
Definition 4.1).
Mizumoto untersucht, welche Arten von Fuzzy Ausgaben man
erhält, wenn man verschiedene Mengen von Fuzzy Eingaben 
in
das
Inferenzsystem 
eingibt.
Seine Erwartung ist
hierbei, daß das Resultat der Fuzzy Inferenz, angewendet auf
eine modifizierte Eingabemenge
, eine ähnliche Modifikation
aufweist wie selbst. Als
,,klassischen''
Spezialfall betrachtet
er die Eingabe der unmodifizierten Menge , woraufhin
die
unmodifizierte Menge 
ausgegeben werden sollte.
Bei Verwendung der Max-Min-Komposition wird seine Erwartung aber nur
für eine geringe Zahl der verwendeten Implikationen erfüllt. Im
,,
Spezialfall'' Gleichheit sind drei Implikationen in der Lage,
die Menge zu reproduzieren.
Verwendet man modifizierte
Eingabemengen, so liefert nur eine Implikation das gewünschte
Ergebnis, allerdings noch nicht einmal bei jedem der verwendeten
Modifikatoren.
Die Max--Komposition
dagegen erhält die Gleichheit für alle Implikationen und
Modifikatoren.
Zur Betrachtung der Ähnlichkeit untersucht Mizumoto
einen bestimmten Modifikator, für
den alle Implikationen die gewünschte Ähnlichkeit liefern. Bei
anderen Modifikatoren seien ähnliche Tendenzen erkennbar. Daraus
schließt Mizumoto, daß die Max--Komposition
besser für die Anwendung in der Kompositionsregel der Inferenz
geeignet ist als die Max-Min-Komposition.
Ezawa und Mizumoto [EM84] formalisieren diese Ergebnisse für den Fall der Max-Min-Komposition. Dazu führen sie zuerst den Begriff der Homomorphie ein:
Diese Eigenschaft ist es, die Mizumoto [Miz84] in seiner oben beschriebenen Untersuchung zu finden erwartet hatte.
Ezawa und Mizumoto sind in der Lage, diese Eigenschaft zu formalisieren:
Auf die Ausführung des Beweises verzichte ich hier.
Aus Satz 4.7 folgt sofort:
Damit sind konkrete Formalismen gefunden, bei deren Einhaltung die Fuzzy Inferenz unter Verwendung der Max-Min-Komposition tatsächlich sinnvolle Ergebnisse liefert.
