Zur Einführung in die Chart-Analyse betrachten wir zuerst den kontextfreien Fall. Dieser ist einfacher, und außerdem nimmt innerhalb der Linguistik in letzter Zeit das Interesse an kontextfreien Grammatiken wieder zu. Das Problem der Mehrdeutigkeiten in den natürlichen Sprachen schränkt die Anwendbarkeit solcher Verfahren aber entscheidend ein. Für die Strukturanalyse natürlicher Sprache werden Verfahren benötigt, die von sich aus keine Einschränkungen erfordern, zum Beispiel bezüglich der Form der Regeln oder der Reihenfolge der Verarbeitungsschritte. Solche Einschränkungen sollten ausschließlich durch die jeweilige linguistische Theorie gegeben sein. Dies schließt die Verwendung einfacher Parsingalgorithmen in vielen Fällen aus. Ein schlichter Top-Down-Parsingalgorithmus ist z. B. ungeeignet, wenn die Grammatik links- oder rechtsrekursive Regeln enthält; simple Bottom-Up-Algorithmen besitzen ähnliche Einschränkungen.
Zur Entwicklung der Chart-Analyse führte außerdem der Wunsch, die Analyse so redundanzfrei wie möglich zu halten. Bei einfachen Verfahren werden nämlich Wortketten, die von mehreren Regeln der gegebenen Grammatik subsumiert werden, auch mehrmals analysiert.
Ein Ansatz zur Lösung dieses Problems besteht in der Speicherung von
Teilergebnissen, die im Laufe der Analyse gewonnen werden. Bei der
Verfolgung alternativer Analysemöglichkeiten kann darauf
zurückgegriffen werden. Diese Teilergebnisse werden in einer Chart
gespeichert. Dies erhöht außerdem die Effizienz der Darstellung
derartiger struktureller Mehrdeutigkeiten, da mehrfach vorkommende
Anteile eines Satzes nur einmal gespeichert werden. Auch das
Backtracking wird effizienter, da bereits bestimmte
Konstituenten![]() nicht mehr gelöscht werden und so dem Backtracking-Algorithmus sofort
zur Verfügung stehen.
nicht mehr gelöscht werden und so dem Backtracking-Algorithmus sofort
zur Verfügung stehen.
Die prinzipielle Methode der aktiven Chart-Analyse wird zuerst an einem Beispiel vorgestellt. Zum Ende dieser Ausarbeitung wird in Kapitel 4 die aktive Chart-Analyse an einem weiteren Beispiel Schritt für Schritt gezeigt.
Wir gehen von folgender kontextfreier Grammatik aus:

Der Satz ,,Der Zug fährt nach Frankfurt'' hat gemäß dieser Grammatik den folgenden Strukturbaum:
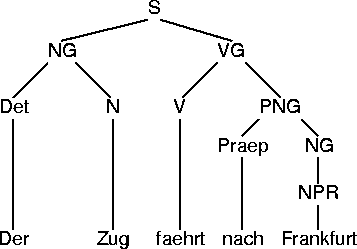
In diesem Baum werden terminale und nichtterminale Symbole als Knoten dargestellt. Bei der Chart-Darstellung werden sie dagegen als Kanten repräsentiert. Um zu dieser Darstellung zu gelangen, wird zuerst der Graph der terminalen Symbole erstellt:
![]()
Dieser Graph wird erweitert, indem immer größere Abschnitte des Satzes mit Kanten überspannt werden, die einem nichtterminalen Symbol entsprechen. Kann eine Kante eingefügt werden, die mit dem Startsymbol S markiert ist und die den ganzen Satz überspannt, ist die Analyse abgeschlossen.
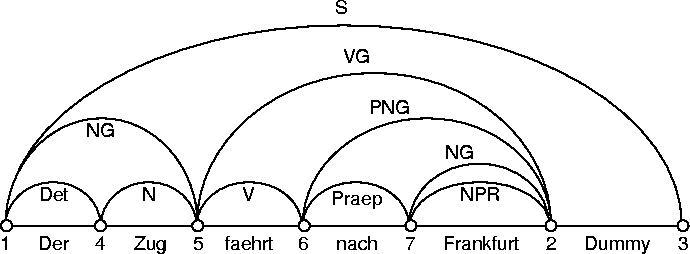
Die Knoten der Chart werden zur leichteren Bezugnahme durchnumeriert. Da am Anfang der Analyse die Zahl der Gesamtknoten noch nicht bekannt ist, erhält der erste Knoten die Nummer 1 und der den Satz rechts begrenzende Knoten die Nummer 2. Dahinter wird, wenn in der Grammatik vorgesehen, eine weitere Kante zwischen Knoten 2 und 3 eingefügt, die mit dem ausgezeichneten Satzende-Symbol Dummy bezeichnet wird. Alle neu hinzukommenden Kanten werden zwischen Knoten 1 und 2 eingefügt, und ihre Knoten werden von links nach rechts durchnumeriert.
Im ersten Schritt wird für jede Kante, die mit einem Terminalsymbol (d. h. einem Wort des Satzes) bezeichnet ist, die entsprechende nicht-terminale lexikalische Kante, die mit der Kategorie des Wortes markiert ist, eingefügt. Diese Wörter sind in der Praxis nicht in der Grammatik selbst, sondern in einem Lexikon abgelegt.
Kann ein Wort mehreren lexikalischen Kategorien zugeordnet werden, so wird eine Kante für jede dieser Kategorien eingefügt (,,Zug'' kann beispielsweise auch ein Städtename sein).

Anschließend werden so lange bereits gefundene Kanten zu neuen (syntaktischen) Kanten kombiniert, bis sich keine weiteren Kanten mehr bilden lassen.
Die in der Analyse konstruierten Kanten enthalten Informationen darüber, welche Knoten sie verbinden und welche Kanten sie subsumieren. In der folgenden Abbildung sind die subsumierten Kanten in eckigen Klammern angegeben:
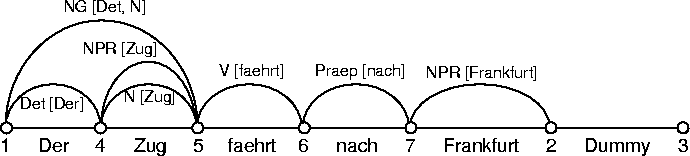
Hier erkennt man die Eignung der Chart, alternative Analysen im Falle syntaktischer Ambiguität kompakt darzustellen, denn die jeweils subsumierten Kanten, die Konstituenten des bereits analysierten Teilausdrucks darstellen, sind in der Chart nur einmal vorhanden.
In der aktiven Chart-Analyse werden zwei Arten von Kanten verwendet: aktive und inaktive Kanten. In den bisherigen Abbildungen wurden nur inaktive Kanten dargestellt, die schon vollständig analysierte Teile des Satzes kennzeichnen. Aktive Kanten werden zur Darstellung noch nicht vollständig analysierter Konstituenten verwendet. Sie überspannen den bereits analysierten Teil der Konstituente und enthalten in ihrer internen Repräsentation Informationen über die Kategorie der gesuchten Konstituente, über die bisher gefundene Teilstruktur und darüber, was noch gefunden werden muß, um die aktive Kante zu vervollständigen und damit in eine inaktive Kante zu verwandeln und sie in die Chart einzufügen.
Zu Beginn der Analyse wird eine leere aktive Kante, d. h. eine Kante, die an demselben Knoten beginnt und endet, am ersten Knoten der Chart eingesetzt und mit dem Startsymbol der Grammatik (S) markiert. Diese Kante stellt eine S-Hypothese dar. Im Verlauf der Analyse werden weitere S-Hypothesen über immer größere Teile des Satzes weitergespannt, bis eine davon ihn vollständig überspannt und damit zu einer inaktiven Kante wird. Damit dieser Prozeß erfolgreich durchgeführt werden kann, muß für jede durch die Grammatik angegebene Teilkonstituente der S-Hypothese rekursiv ein derartiger Prozeß erfolgreich durchgeführt werden.
In unserem Beispiel wird nach der Einfügung der leeren S-Kante eine leere NG-Kante eingefügt, die ihrerseits die Hypothese darstellt, daß ab dem Knoten 1 eine Nominalgruppe gesucht wird, die aus einem Artikel Det und einem Substantiv N bestehen muß. Da die gegebene Grammatik zwei verschiedene Repräsentationen einer Nominalgruppe angibt, wird eine weitere NG-Kante eingefügt, die die Suche nach einer aus einem Eigennamen NPR bestehenden Nominalgruppe repräsentiert.
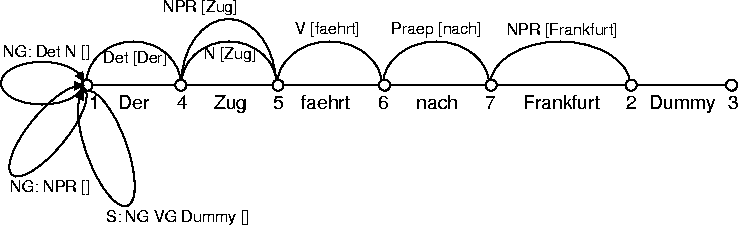
Kann die Analyse nicht erfolgreich durchgeführt werden, so sind im Idealfall (d. h. bei der Verwendung des Bottom-Up-Parsing, siehe Kapitel 2.3) zumindest alle der Grammatik genügenden Konstituenten des Satzes bestimmt und in die Chart eingefügt worden. Damit ist die Technik der aktiven Chart-Analyse auch zur Erkennung von Fragmenten geeignet.
Das ,,Weiterspannen'' aktiver Kanten und das Erzeugen inaktiver Kanten stellen den Kern der aktiven Chart-Analyse dar. Entscheidend ist hierbei die Verknüpfung aktiver mit inaktiven Kanten: Treffen eine aktive und eine inaktive Kante zusammen, kann eine neue, ,,vollständigere'' Kante konstruiert werden. Dies stellt die fundamentale Regel der aktiven Chart-Analyse dar:
Treffen das rechte Ende einer aktiven Kante A und das linke Ende einer inaktiven Kante I in einem Knoten zum ersten Mal zusammen und erfüllt I die Bedingungen von A zur Erweiterung, wird eine neue Kante konstruiert, die A und I überspannt und die Kategorie von A erhält. Ihr Inhalt ist vom Inhalt von A und von der Kategorie und dem Inhalt von I abhängig. Wenn diese Erweiterung A vervollständigt, ist die neue Kante inaktiv, sonst aktiv.
Bei Anwendung dieser Regel auf unser Beispiel (hier nur auf einen Teilausschnitt) wird aus der aktiven Kante NG: Det N[] und der inaktiven Kante Det[Der] eine neue Kante generiert, die von Knoten 1 nach Knoten 4 gespannt wird. Sie wird mit NG: N [Det] bezeichnet und repräsentiert eine partiell instantiierte Nominalgruppen-Hypothese.
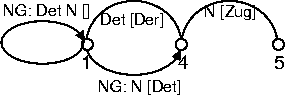
Durch ihre Einfügung kann die Regel erneut angewendet werden, und zwar kann die neue NG-Kante mit der inaktiven Kante N[Zug] verknüpft werden. Das Resultat ist eine neue inaktive Kante zwischen den Knoten 1 und 5, die die komplette Nominalgruppe beschreibt und mit NG [Det N] bezeichnet wird.
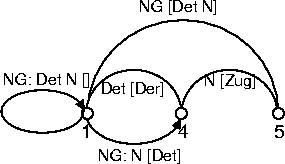
Die Einfügung dieser neuen inaktiven Kante löst in dem abgebildeten Ausschnitt einen weiteren Anwendungsschritt der fundamentalen Regel aus, denn im Knoten 1 treffen die aktive Kante NG: Det N [], mit der das ganze Verfahren begonnen wurde, und die neue inaktive Kante NG [Det N] aufeinander. Die inaktive Kante ist aber zur Erweiterung der aktiven Kante ungeeignet, da sie nicht der Kategorie Det angehört. Daher bricht der Prozeß mit dem oben dargestellten Resultat ab.
Wichtig ist zu bemerken, daß durch Anwendung der fundamentalen Regel keine bereits vorhandenen Kanten modifiziert, sondern immer nur neue Kanten eingefügt werden. Aktive Kanten, die durch eine inaktive Kante erweitert werden, bleiben also auch in ihrem nicht erweiterten Zustand erhalten. Dies scheint redundant zu sein, ist aber eine Voraussetzung zur Behandlung syntaktischer Ambiguität.
Ein weiteres Anwendungsgebiet dieses Verfahrens ist die Analyse gesprochener Sprache, bei der die Ausgangsdaten nicht aus einer Wortfolge, sondern aus einer Menge von zeitlich überlappenden Worthypothesen bzw. Worthypothesenketten bestehen.
Die aktive Chart-Analyse kann im Gegensatz zu einigen anderen Analyseverfahren auch mit linksrekursiven Regeln der Grammatik arbeiten. Bei der aktiven Chart führen linksrekursive Regeln nicht zu einem infiniten rekursiven Abstieg, denn bei jeder neuen Anwendung der Regel wird die Chart um eine neue Kante erweitert, die weiter nach rechts reicht als die bereits existierenden Kanten. Infinite Rekursion ist ausgeschlossen, da jede Kante nur einmal eingefügt wird. Der Prozeß wird also spätestens mit Erreichen des rechten Endes der Chart beendet.
Folgende Eigenschaften der aktiven Chart-Analyse lassen sich also zusammenfassen: