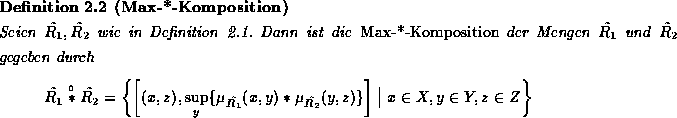
Eine allgemeinere Definition für Kompositionen ist die folgende:
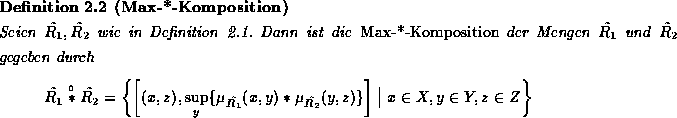
Ist * eine assoziative Operation, die in jedem Argument monoton
wachsend
ist, dann stellt die Max-*-Komposition eine Verallgemeinerung der
Max-Min-Komposition dar.
Ist * eine t-Norm,
so gelten die Gesetze der Assoziativität,
Distributivität und Monotonie genau wie bei der Max-Min-Komposition.
Bei Verwendung des Produkts als Rechenoperation erhält man die
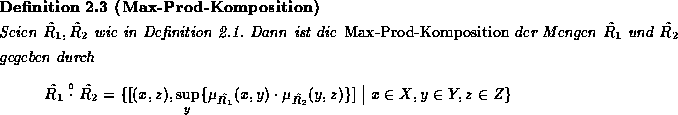
Diese Definitionen werden von Nov·k [Nov89] folgendermaßen
motiviert (S. 71): Die Elemente x und z werden durch die
Elemente
verbunden. Die Stärke dieser Verbindung wird durch
die
stärkste Kette 
bestimmt. Die Stärke
jeder einzelnen Kette wird durch ihr schwächstes Glied festgelegt.
Die Max-Prod-Komposition verfährt nach dem gleichen Prinzip, jedoch werden die Bedeutungen ,,stark'' und ,,schwach'' dabei anders umgesetzt.
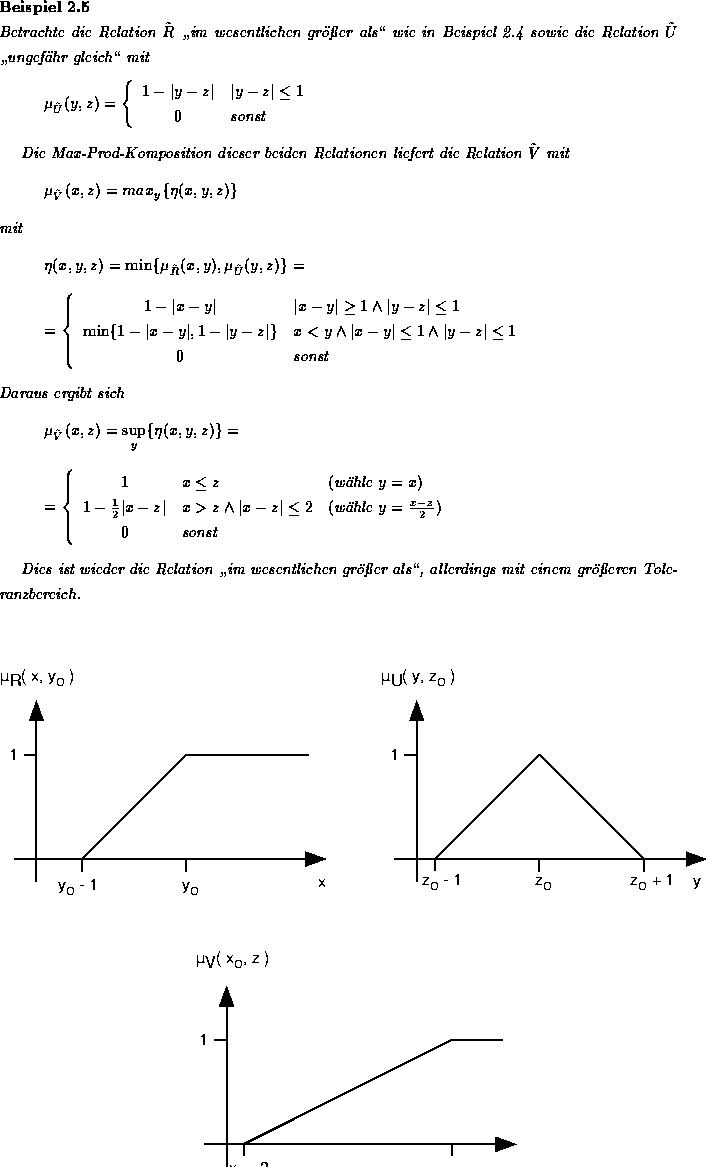
Anhand dieser Beispiele hat es den Anschein, als ob die Max-Min-Komposition sich wie eine logische Oder-Verknüpfung verhält, die unter Umständen noch leichte Modifikationen durchführt. Dies ist natürlich nicht formal bewiesen und stellt nur eine Vermutung meinerseits dar.
