1704 - Rechnerarchitektur
Hauptklausur 1997
Aufgabe K-1:
Man kann mit Petrinetzen die Aufenthaltsdauer einer Marke in einer Stelle P(i) genähert nach Bild K-1 "messen".
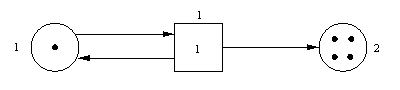
BILD K-1
-
Erläutern Sie Bild K-1, insbesondere auch den maximalen Zeitmeßfehler.
(1 Punkt)
Betrachten Sie zwei unabhängig reparierbare Komponenten (Rechner), die
einzeln mit gleicher Intensität an einer Aufgabe arbeiten, für die ein
Rechner die Dauer d brauchen würde. Zeichnen Sie für folgende Fälle die entsprechenden Petrinetze auf:
-
Wie man die Gesamtrechenzeit (seit dem Einschalten des Systems) messen kann.
(5 Punkte)
-
Wie man erreicht, daß eine Alarmstelle markiert wird, wenn die Dauer d zu spät zustande käme: genauer gesagt nach der Zeit d/2+z, wobei z die Zeitreserve für kurze Ausfälle ist.
(4 Punkte)
Aufgabe K-2:
In ein System von acht würfelförmig vernetzten Rechnern soll ein möglichst "großer" Binärbaum eingebettet werden.
-
Zeichnen Sie räumlich sowie planar ein Beispiel mit möglichst vielen Blättern, wobei im ersteren Bild (Würfel) die Kanten des Baumes fett oder farbig hervorzuheben sind und im letzteren Bild (Binärbaum) nur die o.g. fetten Kanten vorhanden sein sollen.
(3 Punkte)
- Erläutern Sie, warum diese Bäume im wesentlichen gleich aussehen.
(2 Punkte)
- In der Baumspitze soll der Rechner dank einiger interner Redundanz die Unverfügbarkeit U2 haben, alle anderen Knotenrechner sollen die Unverfügbarkeit U haben. Die Kanten (Verbindungsleitungen) sind ideal zuverlässig.
Wie groß ist in quadratischer Näherung (in U) die Systemunverfügbarkeit U, wenn nur die Endknoten (Blätter des Baumes) gemeinsam mit dem Rechner an der Spitze nützliche Arbeit leisten können und zwar mindestens 2 von ihnen.
Begründen Sie Ihre Rechnung ausführlich.
(5 Punkte)
Aufgabe K-3:
Der Zustand der Reparaturwarteschlange eines 3-Komponentensystems sei durch Bild K-2 gegeben.
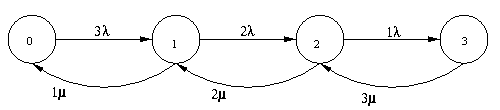
BILD K-2
-
Schreiben Sie die Differentialgleichungen für den Wahrscheinlichkeitsfluß auf.
(3 Punkte)
- Lösen Sie diese Gleichung für den Fall der Stationarität, wenn
P(i) = 0 (gemeint ist Ableitung, also mit Punkt über P) für i ist Element von {0,...,3}.
Beachten Sie dabei die Normierungsregel P(0) + P(1) + P(2) + P(3) = 1.
(4 Punkte)
- Wie lautet die stationäre System-Unverfügbarkeit, wenn die drei
Komponenten speziell ein 2-von-3-System bilden? Das Endergebnis soll als Polynom in der Form U = l / (l + m) dargestellt werden.
(3 Punkte)
Aufgabe K-4:
Schreiben Sie für einen 8bit-Prozessor mit einem Akkumulator A ein
Mikroprogramm DIV, das die Division zweiter 8bit-Zahlen ohne die explizite Verwendung eines Divisionbefehls durchführt. Verwenden Sie den in der Tabelle angegebenen Befehlssatz.
| LOADA X | A <- M(X) | Ladebefehl |
| STOREA X | A -> M(X) | Speicherbefehl |
| SETA X | A := X | Zuweisungsbefehl |
| SUBA X | A := A - M(X) | Subtraktionsbefehl |
| ADDA X | A := A + M(X) | Additionsbefehl |
| JUMP X | PC := X | unbedingter Sprung |
| JUMPN X | PC := X | Sprung, falls N-Flag gesetzt
|
| CMPA X | N-Flag := 0
N-Flag := 1 | für A>=M(X)
für A< M(X)
Verändert nicht den Wert des Akkumulators! |
Der Mikroprozessor besitzt einen internen Speicher, der bei der Adresse X beginnt und bei X+25 endet. Der Dividend und der Divisor stehen im Zwischenspeicher unter der Adresse X bzw. X+1.
Der Quotient und der Divisionsrest stehen im Arbeitsspeicher an den Adressen X+2 und X+3. Dividend, Divisor, Quotient und Divisionsrest sind vorzeichenlose 8bit-Werte. Eine Vergleichsoperation kann nur zwischen einem Register und einer Speicherzelle durchgeführt werden. Speicher-Speicher-Transferoperation sind nicht möglich.
-
Geben Sie zunächst das Flußdiagramm für die Routine an.
(4 Punkte)
- Geben Sie das Mikroprogramm mit ausführlichen Kommentaren an.
(6 Punkte)
Aufgabe K-5:
Entwerfen Sie eine Einheit für einen Mikroprozessor, die die Operation "pusha" und "popa" auf dem Stack (Kellerstapelspeicher) überwacht.
Der Befehl "pusha" erhöht den Stackzeiger SP (Register des Mirkoprozessors) und speichert den Wert des Akkumulators auf der durch den Stackzeiger SP adressierten Adresse ab. Der Befehl "popa" lädt den Wert der Speicherzelle, die durch den Stackzeiger SP adressiert wird, in den Akkumulator und erniedrigt danach den Stackzeiger SP. Der Stack wächst von der niedrigen zur hohen Adresse. Der Stackzeiger SP zeigt auf den zuletzt abgelegten Wert im Stack.
Die Einheit besitzt ein Register OVERFLOW_LIMIT (OVL), welches die obere Grenze im Speicher für den Stack angibt und ein Register UNDERFLOW_LIMIT (UNL), welches die untere Grenze für den Stack angibt, d.h. die unterste Speicherzelle, die für die Ablage eines Wertes auf dem Stack gültig ist (siehe Bild K-3). Für den Fall, daß ein Wert oberhalb der Grenze OVL abgelegt wird, soll ein Signal SIG_OVL den Überlauf des Stacks anzeigen. Für den Fall, daß ein Wert unterhalb der Grenze UNL abgelegt wird, soll dementsprechend ein Signal SIG_UVL den Unterlauf des Stacks anzeigen.
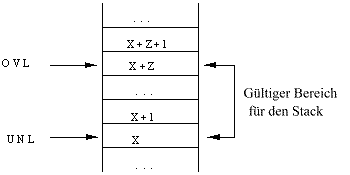
BILD K-3
- Wie lauten die Bedingungen für einen vollen Stack, einen leeren Stack, Stacküberlauf und Stackunterlauf.
(4 Punkte)
- Schreiben Sie für die Operation "pusha" und "popa" jeweils Mikroprogramme. Fügen Sie die Befehle check_ovl und check_uvl an den passenden Stellen ein.
(2 Punkte)
- Zeichnen Sie ein Blockdiagramm für diese Einheit, die die Operationen auf dem Stack überwacht und die obengenannten Signale SIG_OVL und SIG_UVL erzeugt. Als Elemente stehen ihnen Addierer, Negierer, Halbaddierer, Volladdierer und Register zur Verfügung.
(4 Punkte)



