1663 - Datenstrukturen

Hauptklausur 1997 (vom 16.08.97)

Aufgabe 1 (AVL-Baum):

1. Gegeben sei der folgende AVL-Baum

   

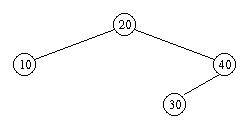
   Fügen Sie nacheinander Knoten mit den Schluüsseln 25, 23 und 35 in den Baum ein. Markieren Sie den betroffenen Knoten, falls das AVL-Kriterium bei einer Einfüge-Operation verletzt wird, und rebalancieren Sie den Baum unter Angabe des Verfahrens. Zeichnen Sie nach jedem Einfügen eines Objektes den Ergebnisbaum.
   (8 Punkte)

2. Gegeben sei der folgende AVL-Baum:

   

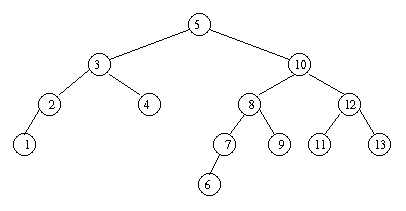
   Löschen Sie aus dem Baum das Element 4. Markieren Sie den betroffenen Knoten, falls das AVL-Kriterium durch das Löschen verletzt wird, und rebalancieren Sie den Baum unter Angabe der notwendigen Rotationen.
   (8 Punkte)

3. Begründen Sie, warum Suchen, Einfügen und Löschen in einem AVL- Baum jeweils in logarithmischer Zeit möglich ist.
   (4 Punkte)

Aufgabe 2 (B-Baum):

1. Erweitern Sie den nachfolgend dargestellten B-Baum der Ordnung 2, indem Sie nacheinander die Schlüsselelemente 40, 60, 30, 73, 31 einfügen. Stellen Sie jeweils diejenigen Bäume dar, für die eine Overflow-Operation durchgeführt werden muß. Geben Sie den Baum an, den man als Ergebnis aller Einfügeoperationen erhält.

   

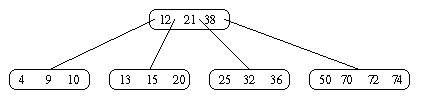
   (9 Punkte)

2. Löschen Sie aus dem nachstehenden B-Baum der Ordnung 2 nacheinander die Schlüsselelemente 36, 83, 35, 70, 50, 15, 46, 84 und 18. Geben Sie an, welche Löschungen zu einem Underflow führen und mit welcher Operation zu reagieren ist, und stellen Sie jeweils den zugehörigen Ergebnisbaum dar.

   

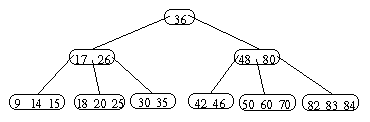
   (9 Punkte)

Aufgabe 3 (Heapsort):

Ermitteln Sie für die in einem Array gegebene Schlüsselfolge 19, 37, 79, 22, 08, 17, 99, 66, 77, 32, 04, 27, 89, 15, 74, 86 den Ausgangsheap (Maximumsheap) sowie die Heaps, die von den ersten drei Schritten des Heapsortalgorithmus aufgebaut werden. Das Ergebnis soll eine aufsteigend sortierte Folge im Array sein. Der Ausgangsheap ist der jenige Heap, der nach der ersten Phase des im Kurs angegebenen Healpsortalgorithmus entsteht (Auffüllphase). Danach folgen die ersten drei Durchläufe von Phase 2 (Sinkphase). Wählen Sie zur Visualisierung der Zahlenfolgen im Array eine partiell geordnete Baumstruktur mit Knoten und Kanten. Markieren Sie die Pfade, entlang denen Zahlen sinken. Kennzeichnen Sie ferner Knoten, die zum sortierten Heap gehören.

Aufgabe 4 (Dijkstras Algorithmus):

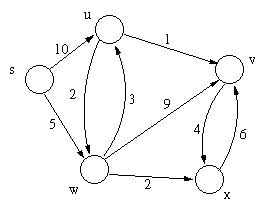
Berechnen Sie im unten gezeigten Graphen mittels Dijkstras Algorithmus die kürzesten Wege vom Knoten s zu allen anderen Knoten. Geben Sie dabei alle Zwischenergebnisse (für jeden Durchlauf durch die while-Schleife) in Form eines markierten Graphen an:

1. Notieren Sie die jeweils aktuellen Kosten in den Knoten.

2. Stellen Sie "grüne" (d.h. expandierte) Knoten grün oder durch Schattieren dar.

3. Zeichnen Sie "rote" Kanten (d.h. Kanten des shortest path tree) rot oder fett.

4. Markieren Sie jeweils den als nächstes grün zu färbenden (d.h. den als nächstes zu expandierenden) Knoten mit einem *.

Aufgabe 5 (Segmentbaum):

Gegeben sei eine Menge {a, ... h} von Intervallen mit
a = [21,56], b = [28,63], c = [28,35], d = [13,49], e = [17,63], f = [35,81], g = [21,49] und h = [49,63].

1. Konstruieren Sie den entsprechenden Segmentbaum. Geben Sie durch Angabe von Intervallgrenzen für jeden Knoten das von ihm repräsentierte Intervall an, und fügen Sie danach die Intervalle a, ... h durch Markieren ein.
   (9 Punkte)

2. Geben Sie alle Intervalle an, die den Wert x = 53 enthalten, und markieren Sie fett oder farbig den Suchpfad.
   (3 Punkte)

Aufgabe 6 (Linksvollständiger Baum):

Ein linksvollständiger Baum ist ein vollständiger Binärbaum, bei dem alle nichtbesetzten Positionen der letzten Ebene rechts von allen besetzten Positionen liegen. Geben Sie einen Algorithmus an, der aus einer Liste einen linksvollständigenBaum in O(n) Zeit konstruiert. ACHTUNG! Verwenden Sie die Algorithmus-Notation aus dem Kurstext, und vermeiden Sie auf jeden Fall PASCAL- oder MODULA-Programme!