Gedächtnisprotokolle 1825

Gedächtnisprotokolle zur Diplomprüfung Logik für Informatiker (Kurs 1825)

Diese Liste ist eine Zusammenfassung von vier Gedächtnisprotokollen, die im Jahr 1995 erstellt wurden.

Aussagenlogik

Wie ist die Menge der Aussagensymbole definiert?
Wie ist die Menge der aussagenlogischen Formeln definiert?
Was versteht man unter einer Belegung?
- Abbildung $\sigma$ : AS -> { 0,1 }
Wie kann diese Funktion zu einer Auswertungsfunktion für aussagenlogische Formeln erweitert werden?
- Definition von < $\sigma$ > : AF -> { 0,1 }
Wieso kann diese Funktion auf diese Weise rekursiv definiert werden?
- Mit der Definition geeigneter Funktionen können die aussagenlogischen Formeln mit Hilfe einer Peano-Algebra erzeugt werden. Damit läßt sich der Rekursionssatz anwenden. Die aussagenlogischen Formeln sind eindeutig zerlegbar, damit ist die Existenz der Funktion h des Rekursionssatzes intuitiv klar.
Wie lautet der Rekursionssatz?
Wie ist die Semantik der Aussagenlogik definiert?
- Durch die Belegung und die Auswertungsfunktion (s. o.)
Was bedeutet im Rahmen der aussagenlogischen Formeln erfüllbar, was allgemeingültig?
Kann die Allgemeingültigkeit einer aussagenlogischen Formel entschieden / bewiesen werden?
- Kann mit der Wahrheitstafelmethode entschieden werden.
Ist die Menge der nicht erfüllbaren Formeln entscheidbar?
- Ja (s. o.)
Welchen Aufwand beansprucht dies?
- Für n Aussagensymbole braucht man mindestens (n-1) * 2^n Elementaroperationen, um die Wahrheitstafel vollständig zu berechnen.
Gibt es schnellere Verfahren?
- Wahrscheinlich nicht, da das Entscheiden der Menge der Tautologien NP-vollständig ist.
Was heißt NP-vollständig?
- P ist die Klasse aller Sprachen, die sich in polynomialer Zeit entscheiden lassen. NP ist die Klasse aller Sprachen, für die ein Beweisverfahren mit polynomialer Rechenzeit existiert. Man weiß bis heute nicht, ob P = NP, aber man glaubt es nicht. Ist das Wahrheitstafelproblem in P, so gilt P = NP.
Wie lautet der Kompaktheitssatz der Aussagenlogik?

Prädikatenlogik

Was ist ein Typ?
Was benötigt man für die Prädikatenlogik?
- Alphabet, Variablen, Funktions- und Prädikatsbezeichner.
Wie sind die prädikatenlogischen Formeln definiert?
Was braucht man zur Semantik der PF noch? / Wie ist die Semantik der PL1 definiert?
- Die Termauswertungsfunktion W und die Wahrheitswertfunktion WW (s. u.)
Wie ist die Belegung definiert?
Wie ist W(t) definiert? / Wie können Terme ausgewertet werden? / Was ist der Wert der Auswertungsfunktion für Terme?
- W : Tm -> (Bel -> S)
Wie ist WW(t) definiert? (Genaue Definition hinschreiben)
- WW : PF -> (Bel -> { 0, 1 })
Definieren Sie für PF die Gültigkeit in Strukturen.
- S 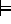$\models$ a( $\sigma$ ) für alle $\sigma$
  Allgemeingültigkeit erhält man durch Quantifizieren über alle Strukturen.
Wann ist eine Formel gültig?
- Wenn es eine Struktur gibt, in der sie gültig ist.
Wann heißt eine prädikatenlogische Formel erfüllbar?
Ist die Menge der allgemeingültigen prädikatenlogischen Formeln rekursiv?
- Nein.
Wie kann man zeigen, daß diese Menge nicht rekursiv ist?
- Durch Reduktion auf das Ableitungsproblem in Semi-Thue-Systemen.
Kann man auch etwas Positives über diese Menge sagen?
- Ja, sie ist rekursiv-aufzählbar.
Genauer Beweis der rekursiven Aufzählbarkeit? Dazu Zwischenfragen:
- Bleibt die Allgemeingültigkeit bei der Allquantifizierung erhalten?
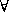
- Warum wird im Beweis die Nichterfüllbarkeit der negierten Formeln ( $\neg$ $\forall$ $\alpha$ ) abgeprüft?
- Was ist eine pränexe Normalform?
- Wie verhält sich eine Formel in Pränexnormalform zur Ausgangsformel?
- Wie funktioniert die Skolemisierung? (an einem Beispiel zeigen)
- Wozu wird die Skolemisierung benötigt? Ist das nicht ein großer Eingriff in die Formel?
  - Die Entscheidbarkeit bleibt erhalten, und man kann sich dann auf die Untersuchung von Herbrand-Modellen beschränken.
- Wie verhält sich die skolemisierte Formel zur Ausgangsformel?
  - Die beiden Formeln sind erfüllbarkeitsäquivalent (nicht äquivalent!)
- Was ist ein Herbrand-Modell, was eine Herbrand-Struktur, was ein Herbrand-Universum?
- Warum Instanzenbildung?
Was ist der Unterschied / der Zusammenhang zwischen der Prädikatenlogik mit und ohne Gleichheit?
Was ist eine Kongruenzrelation?

Theorien

Was ist eine Theorie?
Nennen Sie Beispiele!
- Theorie von N, Gruppenaxiome
Wie lauten die Gruppenaxiome?
Wie kann man Theorien erzeugen?
Ist die Menge der allgemeingültigen prädikatenlogischen Formeln eine Theorie?
- Ja. Die Menge der Konsequenzen einer widerspruchsfreien Menge ist eine Theorie, und die Menge der allgemeingültigen prädikatenlogischen Formeln ist die Menge der Konsequenzen der leeren Menge (die offensichtlich widerspruchsfrei ist).
Sind Strukturen durch eine Theorie festzulegen? (andersherum: Legen Theorien von Strukturen diese eindeutig fest?)
- Nein.
Warum hat Th(N) Y auch ein Modell?
- Argumentation mittels des Kompaktheitssatzes der PL.