Unscharfe Relationen repräsentieren unscharfe Beziehungen zwischen einer festen Anzahl von Objekten. Dieser Vortrag beschränkt sich der Einfachheit halber auf binäre Relationen (also Relationen zwischen zwei Objekten). Die Ergebnisse sind aber leicht auf n-äre Relationen übertragbar.
Binäre Fuzzy-Relationen sind Fuzzy-Teilmengen des Kreuzprodukts
zweier Mengen 
. Sie werden
eingesetzt, wenn man nicht eindeutig sagen kann, ob eine Beziehung
zwischen zwei Elementen besteht oder nicht, sondern wenn man nur
angeben kann, in welchem Maße die Beziehung zwischen den Elementen
besteht. Beispielsweise ist die häufig verwendete Relation ,,viel
kleiner als'' eine Fuzzy-Relation, denn die Aussage ,,
''
hat einen geringeren
Wahrheitsgehalt als die Aussage ,,
''.
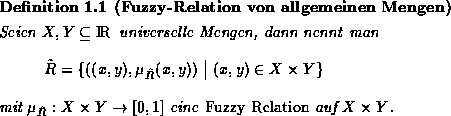
Hierbei weist die Funktion 
jedem Paar 
einen Zugehörigkeitsgrad zur Relation 
zu.
Dieser Zugehörigkeitsgrad liegt zwischen 0 und 1 und beschreibt den
Grad, mit dem die unscharfe Relation auf die Objekte
(x,y)
zutrifft. Dies darf nicht
mit einer Wahrscheinlichkeitsangabe verwechselt werden.
Für diskrete Träger
können die Fuzzy-Relationen
auch durch Tabellen
angegeben werden.
Der Träger einer unscharfen Relation sowie jeder
-Schnitt von bilden eine
gewöhnliche Relation in . Außerdem gelten alle
bisher für unscharfe Mengen
ausgesprochenen Regeln auch für unscharfe Relationen, da letztere nur
einen Spezialfall unscharfer Mengen darstellen (sie sind nämlich
unscharfe
Mengen in Produkträumen).
Ebenso sind alle für unscharfe Mengen erklärten
Verknüpfungen auch auf
unscharfe Relationen anwendbar.
