Fragenkatalog zum Hauptdiplom Informatik - Kurs Parallele Systeme
(Lehrziele in Blau und Kursiv gesetzt!)
KE1 - Maschinenmodelle und Komplexitätsmaße
Welches Rechenmodell wurde im Kurs eingeführt und welche Unterscheidungen gibt es?
- Erläutern Sie die Modelle der RAM und der PRAM!
- Erläutern Sie die Behandlung der Lese-/Schreibkonflikte in den verschiedenen Varianten der PRAM!
Im Kurs wurde das Rechenmodell der RAM und der PRAM eingeführt. Eine RAM (Random Access machine) besteht aus einem
- Eingabeband mit Lesekopf
- Ausgabeband mit Schreibkopf
- Einer potentiell unendlichen Folge von Registern r0, r1, ....
- Einem Programm
- Einem Befehlszähler
Insbesondere sind alle rekursiv berechenbaren Funktionen auf einer RAM realisierbar.
Eine PRAM ist eine RAM erweitert um die Möglichkeit der parallelen Ausführung von Befehlen in vielen Registern gleichzeitig.
Voraussetzung dazu ist:
- PRAM arbeitet synchron in allen Registern (alle Prozessoren arbeiten mit gleichem Takt)
- SIMD Modell (single instruction, multiple data)
- Jeder Prozessor hat Zugriff auf jeden anderen Prozessor
- Jeder parallele Algorithmus kann auch sequentiell ausgeführt werden
Je nach Ausprägung des Speicherzugriffs unterscheidet man:
- EREW PRAM (exclusive read, exclusive write)
- CREW PRAM (concurrent read, exclusive write)
- CRCW PRAM (concurrent read, concurrent write)
- Common CRCW PRAM
Gleichzeitiges Schreiben ist nur dann erlaubt, wenn alle beteiligten Prozessoren den gleichen Wert in ein Register schreiben wollen. Andernfalls liegt ein Programmfehler vor.
- Arbitrary CRCW PRAM
Ein beliebiger Wert von den angebotenen wird ins Register geschrieben (einer gewinnt)
- Priority CRCW PRAM
Unter den beteiligten Prozessoren schreibt derjenige mit der kleinsten Adresse, die anderen werden zurückgewiesen (Natürlich sind andere Regeln zur Konfliktbehandlung und der Prioritätsregelung denkbar)
- Wie sind die Komplexitätsmaße Rechenzeit und Aufwand definiert?
Laufzeit wird mit t(n) bezeichnet, der Aufwand wird über die Anzahl der benötigten Prozessoren p(n) angegeben. Für die Gesamtkosten w(n) gilt: w(n)<=p(n)*t(n)
- Definition der O-Notation?
Seien h,g: N -> R+ Funktionen. Dann bedeutet h
Î O(g) (h ist groß-O von g): Es gibt eine Konstante c>0, so daß für fast alle nÎ N (d.h bis auf endlich viele Ausnahmen) gilt: h(n) £ c × g(n).
M.a.W: 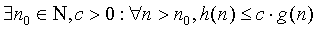 .
.
- Diskutieren Sie die Unterschiede zwischen den Berechnungsmodellen mit verschiedenen Datentypen (ganzzahlig, reell, boolesch), Grundoperationen (arithmetisch, logisch) und Kostenmaßen (uniform, logarithmisch)!
Ganzzahliges Berechnungsmodell ((P)RAM)
uniformes Kostenmaß
- Reelles Berechnungsmodell (real PRAM)
Betrachung von Berechnungsmodellen mit reellen Zahlen mit Hilfe des uniformen Kostenmaßes. Problematisch sind Unstetigkeiten und Singularitäten wie z.B. Tests auf 0 (x=0?, x>0?). Dient zum Studium der kombinatorischen und/oder geometrischen Natur eines Berechnungs-Problems.
- Boolsches Berechnungsmodell (Bit-(P)RAM)
Mit Hilfe dieses Modells kann man die Komplexität eines Berechnungsproblems in Abhängigkeit von der Stelligkeit messen. (Bspw. ist die Komplexität der Grundoperationen Multiplikation/Addition im uniformen Kostenmaß stets O(1)) Bei Bit-(P)RAMs (für Zahlendarstellungen zur Basis 2) sind die Grundoperationen logische Verknüpfungen (das Kostenmaß ist logarithmisch)
- Uniformes Kostenmaß
legt natürliche Zahlen und Rechenschritte als Einheiten zugrunde
- Logarithmisches Kostenmaß
bezieht die Länge der Operanden in das Komplexitätsmaß mit ein
- Gibt es weitere parallele Berechnungsmodelle und welchen Sinn, bzw. welche Vorzüge und Nachteile haben diese?
- Prozessornetzwerke wie z.B. Hypercube oder Gitterarchitekturen. Vorteil: Näher an existierender Hardware, Nachteil: Komplexitätsanalyse schwieriger.
- Boolesche Schaltnetze.
- Was braucht man für das Grundmodell der PRAM?
(siehe 3) Voraussetzungen: parallele RAM, synchroner Takt, SIMD, vollständig vernetzte Prozessoren.
- Ist das PRAM Modell eigentlich realistisch?
(Nein, Prozessorkommunikation hat entscheidenden Einfluß)
KE 2 - Entwurfstechniken
Wie werden Präfixsummen bestimmt? (genau erklären!)
Parallele Berechnung erklären
- Falls die Anzahl der Zahlen in der Folge keine Potenz von 2 ist, wird auf die nächsthöhere 2er-Potenz mit Nullen aufgefüllt.
- Bilde parallel und rekursiv paarweise die Summen (zi) der Zahlen an den ungeraden und den geraden Stellen der Folge (der Algorithmus ruft sich jeweils mit den gebildeten Summen solange selbst auf, bis die Anzahl der Folgenglieder 1 ist)
- Beim Abbau der Rekursionsstufen wird das 1. Glied der übergebenen Folge (x1) jeweils die Präfixsumme s1. Die geraden si sind jeweils die zi/2 aus dem Schritt 2. Die ungeraden Glieder entstehen jeweils durch Addition der geraden Glieder z(i-1)/2 und dem xi aus der übergebenen Ursprungsfolge.
- Laufzeit des Algorithmus ist O(log n) wegen
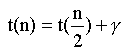 und der Aufwand ist O(n) wegen
und der Aufwand ist O(n) wegen 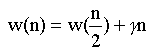
(Beweis mittel vollständiger Induktion über die Anzahl der Summanden)
Präfix"summen" sind auf allen Grundbereichen mit assoziativen Operationen berechenbar.
Wo wird dieser Algorithmus (im Kurs) verwendet?
- Berechnung der Knotenabstände in Bäumen
- Berechnung der Potenzen der w bei der FFT
- vorbereitendender Schritt bei der parallelen Lösung des list-ranking (siehe SA), dabei werden - Listenelemente die in m > n Registern verteilt sind auf die ersten n Register kompaktiert.
- Zur Numerierung der Blätter eines geordneten Bin-Baumes bei der Baumkontraktion.
- Erläutern Sie die Technik des divide-and-conquer!
Bedeutung: Teile und herrsche. Die Technik besteht darin, ein Problem in mehrere etwa gleich große Teilprobleme zu zerlegen, so daß jedes Teilproblem eine ‚einfacher' zu findende Lösung hat (‚divide'). Dann kombiniert man die gefundenen Teillösungen zu einem Gesamtergebnis (‚conquer'). Die Teilprobleme werden wieder in noch kleinere Teilprobleme zerlegt, so daß sich insgesamt eine rekursive Struktur des Algorithmus ergibt.
- Wie gelangt man mittels Rekurrenzungleichungen zu Komplexitätsabschätzungen?
Satz 2.1.4
Seien a,b,c,d,
g reelle Konstanten mit a ³ 1, b > 1, c ³ 0, d ³ 0, g > 0, Eine monotone reelle Funktion t erfülle für n ³ b die Rekurrenz . 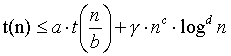
(logdn bedeutet (log2n)d)
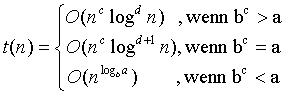 Für t gilt dann folgende Abschätzung:
Für t gilt dann folgende Abschätzung:
- Können Sie einige Standardfälle von Rekurrenzungleichungen lösen?
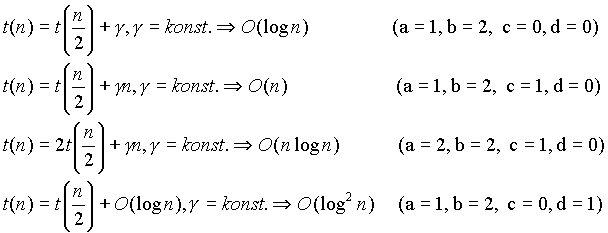
- Wie kann man Zahlen schneller multiplizieren als mit der Schulmethode?
Karatsuba-Ofman (1962) in O(n1.59)=O(nlog3) bzw Schönhage-Strassen (1971) in O(nlognloglogn).
Nach der Schulmethode können zwei n-Bit-Zahlen in n2+2n-1 Zeiteinheiten multipliziert werden, also in O(n2) Zeit. Führt man die Multiplikation von n-Bit- Zahlen auf mehrere Multiplikationen von Zahlen der Länge n/2 (a,b,c,d) bzw. n/2 + 1 (a+b,c+d), sowie auf einige Multiplikationen mit Zweierpotenzen und einige Additionen zurück, dann läßt sich O(nlog3) erreichen. Also:
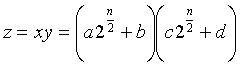
Ausmultiplizieren
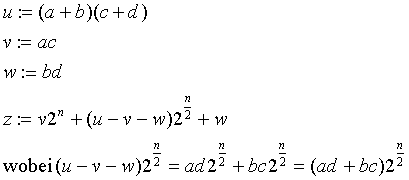
Also gilt: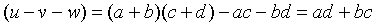
Multiplikationen von n/2-Bit-Zahlen werden durch rekursive Aufrufe des Verfahrens erledigt. Pro Rekursionsstufe werden offenbar drei Multiplikationen von n/2-Bit-Zahlen erledigt. Additionen und Multiplikationen mit Zweierpotenzen sind in O(n) Zeit zu erledigen. (Schulmethode bzw. Shift). Damit ergeben sich folgende Rekurrenzungleichungen:
t(1)
£ k,
t(n)
£ 3t(n/2)+kn
Und daraus folgt mit Hilfe von Satz 2.1.4: O(nlog3). Für den Fall der parallelen Abarbeitung der Rekursionen ergibt sich O(n).
- Was versteht man unter dynamischer Programmierung ? (Beispiele!)
Unter dynamischer Programmierung versteht man das Erzeugen von Teillösungen schrittweise wachsender Teilprobleme. Es handelt sich um eine Technik, die sich in erster Linie zum Entwurf sequentieller Algorithmen eignet. Beispiel:
≤k≤n) durchsucht. Es werden jeweils Folgen Qi gebildet, die Zahlen xi<=xk enthalten und wobei |Qi|≤k ist. Die Folgen Qi werden bei jedem Durchlauf k so angepaßt, daß das erste und das letzte Folgenglied von Qi möglichst klein bleibt (unter Beibehaltung der Monotonie xi ≤ xk bzw. xi≤xi+1)
- sparsames Multiplizieren einer Folge von Matrizen
(In welcher Reihenfolge muß man die M1-Mn multiplizieren um die Anzahl der Mat-Multiplikationen zu minimieren?)
- Erklären Sie genau, wie die parallele Berechnung von Präfixsummen funktioniert!
Siehe 1.
- Erläutern Sie die Beschleunigungstechnik (accelerated cascading) allgemein und am Beispiel!
Bei Problemen mit ‚günstigen' Zerlegungseigenschaften kann durch Kombination eines schnellen oder sogar zeitoptimalen und eines aufwandsoptimalen Algorithmus ein paralleler Algorithmus entstehen der beide Eigenschaften in sich vereint. Beispiel im Kurs ist die Maximumsbestimmung auf einer Zahlenfolge:
- Ansatz mit parallelem Vergleich aller möglichen (n2) Zahlen benötigt zwar nur O(1) Zeit aber O(n2) Aufwand auf einer common CRCW PRAM
- Ansatz mit rekursiver Restklassenbildung j=i mod
ë Ö nû . Dabei wird die Folge in Ö n Teilstücke der Länge Ö n zerlegt und auf diesen das Maximum mit Hilfe des obigen Algorithmus gesucht. Dies erfordert O(loglogn) Zeit und O(nloglogn) Aufwand.
- Beim Einsatz des accelerated cascadings wird die Eingabe in etwa n/loglogn Blöcke der Größe loglogn zerlegt. Die einzelnen Teilprobleme werden - da sie klein und voneinander unabhängig sind - sequentiell gelöst. Das Maximum der Teillösungen wird dann mit Hilfe des vorherigen Algorithmus in O(loglogn) Zeit mit O(n) Aufwand erledigt. (siehe KE2, S.20)
KE 3 - Listen- und Baumoperationen
- Was ist List-Ranking?
Erläutern: Initialisierung, parallele Ausführung der While-Schleife , warum reicht einen EREW-PRAM aus. (weil die Prozessoren nur auf eigene Register schreiben und beim Lesen jeder Prozessor (synchron) aus genau einem anderen Prozessor liest. Dabei ist jedem Prozessor genau ein oder kein (Ende der Liste) Partner zugeordnet.
Unter dem Rang eines Listenelementes versteht man dessen Abstand zum Ende der Liste (Das letzte Element einer n-elementigen Liste hat den Rang 0 und das erste Element hat den Rang n-1). Das Problem insgesamt wird List-Ranking genannt. Die Lösungsstrategie die der vorgestellte parallele Algorithmus verfolgt, wird Verdoppelungstechnik oder 'Pointer-jumping' genannt.
Erläuterung:
Seien n Listenelemente in n Prozessoren gespeichert. Jeder Prozessor i kennt nur seinen Nachfolger si in der Liste, nicht jedoch seinen Listenindex. Jedes Listenelement sei mit einer Variablen ri für den Rang ausgestattet und diese Variable sei mit 1 initialisiert (bis auf das letzte Element (si=0) das mit 0 initialisiert wird). Jedes Element sei außerdem mit dem Hilfszeiger qi versehen welcher mit si initialisiert wird. Die ab dem Knoten i gespeicherte Liste wird nun in einer while-Schleife durchsucht indem man den Hilfszeiger qi als Laufzeiger benutzt (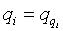 ). Für jeden erfolgreichen Schritt für den
). Für jeden erfolgreichen Schritt für den 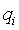 und
und 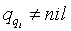 sind, wird der Rang ri von i um
sind, wird der Rang ri von i um 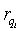 erhöht. Da das ganze parallel für alle Listenelemente abläuft, springt
erhöht. Da das ganze parallel für alle Listenelemente abläuft, springt 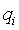 für jeden Durchlauf k der while-Schleife auf das 2k te Listenelement von i aus betrachtet. Die ri wachsen ebenso potentiell zur Basis 2. D.h. nach dem Durchlauf k der while-Schleife sind 2k Elemente mit dem korrekten Rang versehen. Alle höheren Ränge sind bis vorerst mit dem Rang 2k versehen. Paralleles List ranking benötigt O(log n) Zeit mit O(n log n) Aufwand auf einer EREW PRAM.
für jeden Durchlauf k der while-Schleife auf das 2k te Listenelement von i aus betrachtet. Die ri wachsen ebenso potentiell zur Basis 2. D.h. nach dem Durchlauf k der while-Schleife sind 2k Elemente mit dem korrekten Rang versehen. Alle höheren Ränge sind bis vorerst mit dem Rang 2k versehen. Paralleles List ranking benötigt O(log n) Zeit mit O(n log n) Aufwand auf einer EREW PRAM.
Wie kann man parallel arithmetische Ausdrücke auswerten?
Verfahren erläutern: Eulerkreis, Baumkontraktion, Werterhaltung beim RAKE, etc. - Warum kann man nicht den Baum auswerten, indem man die benachbarten Blätter parallel auswertet?
Man kann! Es funktioniert, aber die Anzahl der Knoten wird nicht mehr halbiert. Damit verliert man die logarithmische Zeitschranke.
- Wie berechnet man Abstände in Bäumen?
Gerichteten Baum per Eulerpfad bestimmen durch Konstruktion eines Eulerpfades von r nach r:
Der Rang der Kanten im Eulerpfad wird mittels List ranking ermittelt. Da der Rang von p(v)->v größer ist als der von v->p(v) ergibt sich aus dem Kantenrang unmittelbar die Anordnung der Kanten im gerichteten Baum,
- Kanten des Eulerpfades mit List-Ranking durchnumerieren (was schon im ersten Schritt geschehen ist)
- Den Kanten die Gewichte +1[p(v)® v] bzw. -1[v® p(v)] zuordnen
- Präfixsummen der Kantengewichte bestimmen
Der Abstand eines Knotens vÎ V von einem festen Knoten r ist berechenbar in O(log n) Zeit mit O(LR(n)) Aufwand auf einer EREW PRAM. Die paarweisen Abstände aller Knoten in einem Baum sind in O(log n) Zeit mit O(n LR(n)) Aufwand berechenbar.
Erläutern Sie das list-ranking-Problem und seine O(n log n)-Lösung mittels pointer jumping!
Können Sie die im Kurs genannten graphentheoretischen Definitionen wiedergeben?
Ein (ungerichteter) Graph ist ein Paar G=(V,E). V ist eine endliche Menge, deren Elemente Knoten heißen. E ist einen Menge von Kanten, d.h. von ungeordneten Knoten aus V.
- Ein Graph T=(V,E) ohne Kreise heißt Baum. Ein gerichteter Graph oder Digraph (von directed graph) ist ein Paar D=(V,F) wobei F jetzt eine Menge von geordneten Paaren von Knoten ist; man spricht auch von gerichteten Kanten.
- Ein Eulerkreis in einem Digraphen D=(V,F) ist eine Folge von gerichteten Kanten v1 -> v2 ->......-> v|F| -> v1 die jede Kante von F genau einmal enthält und zum Ausgangsknoten zurückkehrt. (Dagegen dürfen Knoten mehrfach besucht werden, d.h. die obigen vi sind im allgemeinen nicht alle verschieden.)
- Ein Baum-Digraph ist ein Baum T=(V,E) in dem man jede Kante uv
å E durch zwei gerichtete Kanten u->v und v->u ersetzt.
- Sei D ein Baum-Digraph mit n Knoten und u->v eine beliebige Kante. Dann bildet die Folge der sk(u->v) mit k=0,...,2n-3 einen Eulerkreis in D.
- Wie wird in einem Baum Digraphen ein Eulerkreis parallel konstruiert?
Zum besseren Verständnis hier zunächst die Vorschrift zur sequentiellen Konstruktion eines Eulerkreises:
Jeder Baumdigraph besitzt einen Eulerkreis. Satz von Euler-Hierholzer:
Jeder zusammenhängende Graph mit geradem, positiven Knotengrad ist ein Eulerscher Graph.
Konstruktion des Eulerkreises mittels:
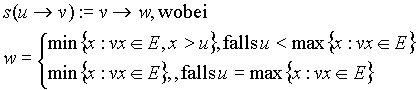
Der Nachfolger einer Kante u->v ist die Kante v->w, wobei w>u sein muß falls u kleiner ist als der maximale Knotenwert x aller Nachbarn von v. Falls u selbst schon maximal ist unter seinen Nachbarn, dann wird dasjenige w mit v->w genommen, daß das minimalste unter den w's ist.
Parallele Konstruktion des Eulerkreises: Zunächst muß der Baum durch folgende Datenstruktur repräsentiert sein: Die Nachbarn jedes Knotens v, also die Knoten x mit vx
Î E, werden jeweils zu einer zyklischen Liste verbunden. Für jede Kante uvÎ E steht dann insbesondere u in der Liste von v und umgekehrt. Diese beiden Listenelemente werden außerdem noch gegenseitig durch Zeiger verbunden. Will man jetzt s(u->v)=v->w berechnen, muß man vom Listenelement v in der Liste von u aus nur zwei Zeiger verfolgen: Erstens zum Listenelement u in der Liste von v, und und zweitens von dort aus zum zyklischen Nachfolger von u in der Liste von v. Dies geht parallel - wegen fehlender konkurrierender Lese-/Schreibzugriffe - auf einer EREW PRAM in O(1) Zeit mit O(n) Aufwand.
- Können Sie die Eulerkreistechnik auf die Abstandsberechnung in Bäumen anwenden?
Bestimmung eines gerichteten Baumes mit Hilfe der Eulerkreistechnik
Dazu wird ein Eulerpfad zwischen einem festen Knoten r und einem Knoten v
Î V konstruiert, wobei jeder Kante p(v)->v das Gewicht +1 und jeder Kante v->p(v) das Gewicht -1 zugeordnet wird. Durch list ranking sind die Kanten im Eulerpfad bereits durchnumeriert. Berechnet man nun die Präfixsummen der Kantengewichte, dann ist der Abstand zwischen r und v genau gleich der Präfixsumme an der Stelle p(v)->v.
- Was versteht man unter der RAKE-Operation und was versteht man unter Baumkontraktion?
Sei T ein Binärbaum mit Wurzel r. p(v) bezeichne den Vater des Knotens v
¹ r. Mit sib(v) wird der eindeutig bestimmte Knoten u mit p(u)=p(v) bezeichnet. Die Operation RAKE angewandt auf ein Blatt v von T mit p(v) ¹ r soll folgendes bewirken:
Lösche v und p(v) aus T und setze p(sib(v)):=p(p(v)).
- Beschreiben Sie die Ideen zur parallelen Auswertung arithmetischer Ausdrücke mit Hilfe der Baumkontraktion
Zunächst wurde das parallele Verfahren zur Kontraktion geordneter binärer Bäume eingeführt:
Die Numerierung der Blätter wird mit Hilfe eines Eulerpfades der anstelle der Kanten die Knoten enthält bewerkstelligt. Blätter kommen in diesem Pfad nur einmal vor und erhalten das Gewicht 1; alle anderen Knoten erhalten das Gewicht 0. Präfixsumms über die Blätter schafft (preorder-)Numerierung in O(log n) Zeit mit O(LR(n)) Aufwand.
Zur Konstruktion des preorder-Eulerpfades: Die Ordnung der Knoten ist linker, rechter Sohn, Vater. Startknoten ist Kante von Wurzel zu rechtem Sohn.
Gegeben sei ein geordneter Binärbaum in dem die Blätter bereits in Preorder-Reihenfolge durchnumeriert sind. Rake kann dann sofort simultan auf alle Blätter die linke Söhne sind und ungerade Nummern tragen, angewendet werden. Danach kann Rake auf alle übrigen Blätter mit ungerader Nummer angewendet werden. Halbiert man dann die (geraden) Nummern der verbliebenen Blätter ergibt sich wieder ein korrekt numerierter Baum mit halbierter Anzahl Blätter. Man kann dieses Vorgehen solange fortsetzen bis nur noch der triviale Baum (Wurzel und zwei Blätter) übrigbleibt. Die anfängliche Numerierung der Blätter ist mit Hilfe der Eulerkreistechnik berechenbar in O(log n) Zeit mit LR(n) Aufwand auf einer EREW PRAM, die Rake Schritte erfordern O(log n) Zeit und O(n) Aufwand denn bei jeder Anwendung halbiert sich die Anzahl der Blätter und somit ist man nach log n Runden fertig. Insgesamt ist die Baumkontraktion in O(log n) Zeit und mit LR(n) Aufwand auf einer EREW PRAM ausführbar.
Voraussetzung zur Auswertung arithmetischer Ausdrücke mittels Baumkontraktion ist, daß zu Beginn die Operanden in den Blättern stehen und die Operatoren jeweils in den Knoten des Baumes stehen.
Zur Auswertung von arithmetischen Ausdrücken läßt sich die Kontraktion einsetzen wenn folgende Bedingung bei jedem Rake-Schritt eingehalten wird:
Sei u ein Knoten mit Söhnen v,w. Dann gilt val(u) = (av
× val(v)+bv) o (aw × val(w)+bw), wobei o Î {+,× } die in u stehende Operation ist. Jeder Knoten wird mit einem Paar von Konstanten (av, bv) versehen. Zu Beginn wird v(av, bv) = (1,0) gesetzt. Mit Hilfe obiger Bedingung und der beiden Hilfsvariablen in jedem Knoten wird sichergestellt, daß beim Anwenden der Operation RAKE auf ein Blatt v der Teilausdruck mit der Wurzel sib(v) dann auch zur Verfügung steht. D.h. beim RAKE eines Blattes v (das linker Sohn von u ist), fällt ein Zwischenergebnis an, nämlich in Abhängigkeit von der Operation o in u ({+,× }). Dieses Zwischenergebnis hat einen von val(w) - dem Wert des rechten Sohnbaumes von u abhängigen Teil un einen konstanten Teil. Ersterer landet in aw und letzterer in bw des rechten Sohnknotens w.
Ein arithmetischer Ausdruck der Länge n ist somit in O(logn) Zeit mit LR(n) Aufwand auf einer EREW PRAM auswertbar.
- In jedem der hier besprochenen Algorithmen erklären Sie bitte wo und warum welche früheren Techniken benötigt werden!
Was braucht man zur Auswertung arithmetischer Ausdrücke?
Rake, Blätter numerieren? Wie macht man das?
(Baumkontraktion, Blättern Gewichte zuordnen->Eulerkreis->Präfixsummen. Das mit (Av,Bv) war nicht en detail gefragt, aber mit welchen Operationen geht das (die Auswertung) überhaupt? Antwort: Mit beliebigen kommutativen Ringen, d.h. die Operationen müssen die Kommutativ-, Assoziativ-, und Distributivgesetze erfüllen.
KE 4 - Matrixoperationen
- Wie werden Matrizen effizient multipliziert?
- Strassen-Algorithmus erläutert
- Komplexität: M(n)=O(nlog27)=O(n2.82)
Wegen 7 Matrizenmultiplikationen und 18 Additionen und Subtraktionen auf jeder Rekursionsstufe gilt M(n)=7M(n/2)+18(n/2)2.
- Zerlegungsidee zur Verbesserung auf O(n2.38) Coppersmith/Winograd (1986)
Paralleler Strassen kostet O(log n) Zeit auf EREW PRAM
Geht das auch mit Matrizen, die als Elemente nur Null und Eins enthalten, mit der Addition modulo 2?
Ja! Kernaussagen von Satz 4.1.2 zitieren. In O(M(n)) Zeit mit O(M(n)) Operationen mit Zahlen der Größe höchstens n. Der Trick ist, die Elemente der beiden Matrizen als Elemente von Restklassen modulo n+1 aufzufassen. Denn diese bilden im Gegensatz zu {0,1, Ù ,Ú } einen Ring, auf den der Strassen Algorithmus anwendbar ist. Aus dem Matrixprodukt über dem Restklassenring kann man das Boolsche Produkt unmittelbar herstellen indem man alle auftretenden positiven Elemente im Produkt gleich 1 setzt. Man könnte auch von ganzen Zahlen ausgehen, doch können dann bei den Rekursionen große Zahlen auftreten die den Aufwand verschlechtern.
Ist der Algorithmus für boolsche Matrizen parallelisierbar?
Erklären Sie (im Prinzip) wie man Matrizen parallel und mit weniger als O(n3) arithmetischen Operationen multiplizieren kann!
Um das Produkt von zwei mxm Matrizen zu berechnen, muß man m2 Skalarprodukte von Vektoren mit m Komponenten auswerten, das bedeutet bei naiver Vorgehensweise m3 Operationen.
Zur Verbesserung der Komplexität soll der Strassen-Algorithmus eingesetzt werden:
Zunächst wird, falls m keine 2er Potenz ist auf die nächsthöhere 2er Potenz n>m mit 0-Zeilen und 0-Spalten nach rechts und unten aufgefüllt. Dann werden die beiden Multiplikanten in je 4 n/2 x n/2 Matrizen zerlegt. Insgesamt verringert sich durch die Rechenvorschrift die Zahl der erforderlichen Multiplikationsschritte von 8 auf 7 bei 18 Additionen pro Multiplikation von n/2 x n/2 Matrizen. Wendet man dieses Verfahren rekursiv an, dann ergibt sich die Rekurrenz M(n)=7M(n/2) + 18(n/2)2 mit der Lösung M(n)=O(nlog27) = O(n2.82)
Dieses Verfahren läßt sich parallelisieren in dem man auf jeder Stufe der Rekursion alle Multiplikationen parallel ausführt, wobei sich die Rekurrenz t(n)=t(n/2)+y (y konstant) mit der Lösung t(n)=O(log n) ergibt. Es genügt eine EREW PRAM, da man in O(1) genügend Teilkopien der Teilmatrizen vor Beginn jedes Rekursionsschrittes anfertigen kann.
- Wie kann man die Inversion von Dreiecksmatrizen und beliebigen reellen Matrizen sowie die Lösung linearer Gleichungssysteme auf die Multiplikation von Matrizen zurückführen?
Es sei Ax=b. Dann ist A-1x=b. A habe Dreiecksgestalt. Dann läßt sich das Inverse von A in O(M(n)) Zeit berechnen. D.h. in O(log2n) Zeit auf einer EREW PRAM bei paralleler Ausführung der Inversion von A.
- Wie definiert man lineare Rekurrenzen und was sind hierfür wichtige Beispielklassen?
Beispiele: Polynomauswertung (Horner Schema), Lineare Gleichungssysteme mit beschränkter Bandweite
Beispiel Horner Schema:
Es sei 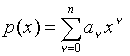 ein Polynom. In Klammerschreibweise erhält man p(x)=a0+x(a1+x(a2+.....+x(an)..)). Löst man diese Klammern von innen nach außen rekursiv auf, erhält man eine lineare Rekurrenz:
ein Polynom. In Klammerschreibweise erhält man p(x)=a0+x(a1+x(a2+.....+x(an)..)). Löst man diese Klammern von innen nach außen rekursiv auf, erhält man eine lineare Rekurrenz:
Y0=an
Y1=y0x+an-1
yi=yi-1x+an-i , (0
£ i £ n)
Diese Rekurrenz ließe sich mit DAC (7) bzw. Satz 4.5.4 in O(log n) Zeit mit O(n) Aufwand lösen. (O(n2) bei paralleler Auswertung an n Stellen).
- Wie lassen sich lineare Rekurrenzen optimal parallel lösen?
Eine lineare Rekurrenz erster Ordnung ist lösbar in O(log n) Zeit mit O(n) Aufwand auf einer EREW PRAM. Und zwar durch Einsatz eines rekursiven Algorithmus, der für jede Rekursionsstufe die Größe der linearen Rekurrenz halbiert.
KE 5 - Fourier-Transformation und Polynomoperationen
Wie kann man parallel effizient Polynome multiplizieren?
Zusammenhang zwischen Konvolution, Fourier-Transformation, FFT (Aufteilung in Teilprobleme) und die Komplexität erläutern. (Äquivalenz von Konvolution und Polynommultiplikation) Funktioniert Polynommultiplikation mit FFT und Konvolution auf jedem Ring?
Nein, w , w -1 und n-1 müssen Elemente des Ringes sein. Auf Körpern funktioniert es immer, denn die sind kommutative Ringe mit Eins-Element und somit existieren n-1 und w -1 immer. Wie sind primitive Einheitswurzeln und die (inverse) Fourier Transformation definiert und wie ist ihr Zusammenhang zu Polynomen?
Ein Element
w Î R (R ist eine Ring) heißt eine primitive n-te Einheitswurzel, wenn gilt:
- w
¹ 1,
- w
n = 1,
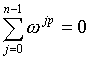
für alle p mit 0 < p < n.
Ein
w , das nur (2) erfüllt, heißt n-te Einheitswurzel.
Was versteht man unter der Konvolution von Vektoren?
Die Konvolution zweier Vektoren a=(a0,....,an-1)T und b=(b0,....,bn-1)T ist der Vektor
c=(c0,...,c2n-1)T mit 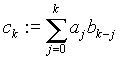 , wobei aj, bj
, wobei aj, bj
³ 0 gesetzt werden falls j ³ n ist.
Was versteht man unter (diskreter) Fouriertransformation und wie hängt sie mit der Polynommultiplikation zusammen?
Der Vektor 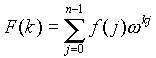 wobei
wobei
w die n-te primitive Einheitswurzel ist, heißt Fouriertransformierte von f. Kompakter kann man schreiben:
Fk=Fa, wobei F die nxn Matrix ist die in Zeile i und Spalte j (0
≤i,j≤n) jeweils das Element w ij enthält. Zeilen und Spalten werden dabei ab 0 gezählt. Sind die Elemente a0,....,an-1 des Vektors a die Koeffizienten des Polynoms 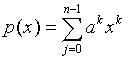 , so gibt Fa offenbar die Werte von p an den Stellen w 0, w 1,....., w n-1 an, denn die i-te Komponente von Fa lautet
, so gibt Fa offenbar die Werte von p an den Stellen w 0, w 1,....., w n-1 an, denn die i-te Komponente von Fa lautet 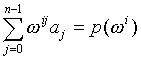 . Ist umgekehrt b der Vektor, der Werte eines Polynoms an den Stellen w i (d.h. bi=p(w i)) dann ist F-1b der Vektor der Koeffizienten von b.
Erläutern Sie den rekursiven FFT-Algorithmus und analysieren Sie ihn!
. Ist umgekehrt b der Vektor, der Werte eines Polynoms an den Stellen w i (d.h. bi=p(w i)) dann ist F-1b der Vektor der Koeffizienten von b.
Erläutern Sie den rekursiven FFT-Algorithmus und analysieren Sie ihn!
Zu einem Vektor a soll b=Fa berechnet werden. Zur Beschleunigung der Berechnung berechnet man die geraden und ungeraden Komponenten von b getrennt:
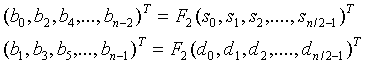
wobei sk=ak+an/2+k und dk=
w k(ak-an/2+k) gesetzt ist. F2 bedeutet hier die Fouriertransformation in n/2 Dimensionen bezgl. w 2. Dadurch ist das Problem zurückgeführt auf zwei Probleme mit halber Dimension. Sind alle w k schon vorher bekannt, erfordert es nur noch linear viele Additionen und Multiplikationen, die für sk, dk parallel ausgeführt werden können. Es gilt t(n)=t(n/2)+O(1) und w(n)=2w(n/2)+O(n), also t(n)=O(logn) und w(n)=O(nlogn) auf einer EREW PRAM.
Wie kann man mit Hilfe des FFT-Algorithmus Polynome multiplizieren und warum kann man diese Idee nicht unmittelbar auf die Multiplikation von Binärzahlen übertragen?
Unmittelbar nicht, weil das System {(0,1),
Ù ,Ú } kein Ring ist. Aber bei Wahl eines geeigneten endlichen Restklassenringes (mod n+1) gelingt dies.
Sind p und q Polynome  und
und 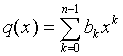 , so gilt (p∙q)(x)=p(x) q(x)=
, so gilt (p∙q)(x)=p(x) q(x)= 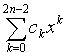 .
.
Die Multiplikation von Polynomen ist äquivalent der Konvolution von Vektoren (nämlich der Koeffizentenvektoren der Polynome). Die Konvolution wiederum kann nach Satz 5.3.2 berechnet werden in O(logn)Zeit mit O(nlogn) Aufwand auf einer EREW PRAM wie folgt: Man berechnet zunächst die Fourier-Transformierte der beiden mit Nullen auf die doppelte Länge verlängerten Koeffizientenvektoren und danach das komponentenweise Produkt dieser beiden Transformierten. Anschließend bildet man davon die inverse Fouriertransformierte:
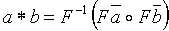
Erläutern Sie, welche effizienten Operationen mit Toeplitzmatrizen behandelt wurden und wie man diese für die parallele Polynomdivision ausnutzt!
Behandelt wurde die Multiplikation von Toeplitz-Matrizen mit einem Vektor. Dies kann in O(log n) Zeit mit O(n log n)Aufwand auf einer EREW PRAM berechnet werden. Das Inverse einer Toeplitzmatrix die zugleich untere Dreiecksmatrix ist, kann in O(log2n) Zeit mit O(n log n) Aufwand auf einer EREW PRAM berechnet werden. Form dieser Matrix (für n=4):
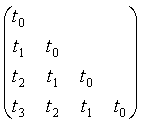
Das heißt eine Toeplitzmatrix in unterer Dreiecksgestalt ist durch ihre erste Spalte (einen Vektor) vollständig charakterisiert. Deshalb kann der Aufwand hier unter n2 liegen, was ja normalerweise allein zum Hinschreiben schon benötigt würde!
Die Inversion einer Toeplitzmatrix in unterer Dreiecksform wird eingesetzt, um Quotient und Rest zweier Polynome vom Grad n in den obigen Zeit- und Aufwandsgrenzen zu berechnen. Dies geschieht indem man zu gegebenen Polynomen 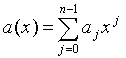 und
und 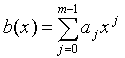 , n>=m mit Hilfe der eindeutig bestimmten Polynome q(x) und r(x) (Quotient und Rest) den Ausdruck a(x)=q(x)b(x)+r(x) bildet. Dabei ist grad(r)<grad(b). Es gilt also q(x)b(x)=a(x)-r(x) und damit wegen der Äquivalenz zwischen Konvolution und Polynommultiplikation
, n>=m mit Hilfe der eindeutig bestimmten Polynome q(x) und r(x) (Quotient und Rest) den Ausdruck a(x)=q(x)b(x)+r(x) bildet. Dabei ist grad(r)<grad(b). Es gilt also q(x)b(x)=a(x)-r(x) und damit wegen der Äquivalenz zwischen Konvolution und Polynommultiplikation 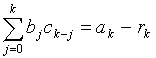 . Für k >= m-1 sind die rk offenbar null und man erhält das Gleichungssystem:
. Für k >= m-1 sind die rk offenbar null und man erhält das Gleichungssystem:
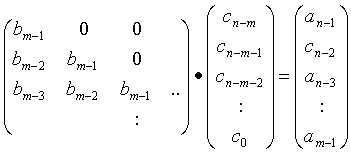
Skizzieren Sie die rekursiven Algorithmen zur Polynomauswertung an n Stellen und die Polynominterpolation!
Parallel ausgeführtes Hornerschema: Also 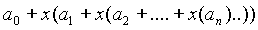 . Dies führt auf folgende lineare Rekurrenz:
. Dies führt auf folgende lineare Rekurrenz: 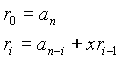 . Benötigt O(logn) Zeit und O(n2) Aufwand.
. Benötigt O(logn) Zeit und O(n2) Aufwand.
Polynomauswertung an n Stellen mit Hilfe der Polynomdivision
O(log3n) Zeit und O(nlog2n) Aufwand
Polynominterpolation mit Hilfe der Lagrange Polynome
O(log3n) Zeit und O(nlog2n) Aufwand.
KE 6 - Sortieren und Suchen
- Erklären Sie den Unterschied zwischen lexikographischen Sortieren und Sortieren durch Vergleiche!
Lexikographisches Sortieren ist ein Beispiel für ein Sortierproblem, wo die zu sortierenden Elemente eine innere Struktur besitzen. Beim Sortieren durch Vergleiche werden die zu sortierenden Elemente jedoch als Atome aufgefaßt, wobei die einzige Grundoperation im direkten Vergleich zweier Elemente besteht; also x<y, x=y, x>y.
- Erläutern Sie das lexikographische Sortieren in Linearzeit!
Für dieses Problem wird Bucketsort eingesetzt. Man durchläuft die n gegebenen Wörter (der einheitlichen Länge l) von hinten nach vorne. Beim j-ten Durchlauf der insgesamt l Durchläufe wird jedes Wort in die entsprechende Schlange gemäß seinem (l+1-j)-ten Symbol eingeordnet. Nach l Durchläufen ist dann die lexikographische Sortierung hergestellt. Insgesamt kann eine Menge von Wörtern der Gesamtlänge n, mit Symbolen aus dem Alphabet [O,m) in O(n+m) Zeit lexikographisch sortiert werden.
- Begründen Sie die untere Schranke für das Sortieren durch Vergleiche!
Jeder Sortieralgorithmus benötigt mindestens a*nlogn Vergleiche (a<1), also gehört mindestens zu O(n log n).
Begründung: Ein n-elementige Menge besitzt n! mögliche Permutationen. Die Anzahl der mögliche Lösungen kann durch jeden Vergleich höchstens halbiert werden und damit gibt es eine Eingabe die log2n! Vergleiche erzwingt, um eine richtige Permutation zu finden. Mit Hilfe der Stirlingschen Formel 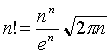 erhält man log2n!=n log n-O(n).
erhält man log2n!=n log n-O(n).
- Geben Sie den einfachen parallelen Mergesortalgorithmus mit O(log2n) Zeit an!
Zunächst wird das merging auf das ranking-Problem zurückgeführt. Es sei rank(x:A)=max{j:aj<x} und rank(B:A)=(r1,...,rm) mit ri = rank(bi:A). Offensichtlich ist rank(x:C)=rank(x:A)+rank(x:B). Man kann also aus rank(A:B) und rank(B:A) in O(1) Zeit mit O(n+m) Aufwand rank(x,C) berechnen. Aus den Zahlen rank(x:C) läßt sich C sofort aufstellen. Würde man das Verfahren jetzt parallel auf alle x=bi anwenden, so käme man auf einen Aufwand von O(mlogn) (bei binärem Suchen) was für m>n/logn und für n=m schlechter wäre als das sequentielle Verfahren. Durch eine geschickte Zerlegung des Problems in m/logm Blöcke A(i) und B(i) der Größe logm so daß gilt |B(i)|
» log m und jedes Element von A(i)È B(i) größer ist als jedes Element von A(i-1)È B(i-1), erreicht man, daß das Merging zweier Folgen in O(logn) Zeit mit O(n) Aufwand auf einer CREW PRAM möglich wird: Ist | A(i)| ≤ log n dann vermischt man A(i) und B(i) einfach sequentiell ansonsten wendet man das Verfahren rekursiv auf die Folgen A(i) und B(i) an. Über alle merging Vorgänge betrachet also O(loglogn) Zeit und O(nlogn) Aufwand für das Sortieren mit Mergesort.
- Erläutern Sie die parallele Suche mit Hilfe von p Prozessoren in einer sortierten Folge!
Man läßt die Prozessoren im Abstand n/p auf die sortierte Folge zugreifen und vergleicht pn-1<x<pn. Das heißt, man sucht dasjenige n/p-lange Intervall der sortierten Folge, das x enthält. All dies ist in O(1) Zeit auf einer CREW PRAM möglich. Das Verfahren läßt sich rekursiv auf das Trefferintervall anwenden bis der Index von x zurückgegeben wird, man wird also in O(logpn) Schritten fertig.
- Beschreiben Sie die wesentliche Idee, die zu einem schnelleren parallelen Sortieralgorithmus führen!
Durch binäres Suchen kann man rank(x:A) in O(logn) Zeit bestimmen. Hat man mehrere Prozessoren können diese parallel suchen ( siehe oben). Dann ist rank(B:A) berechenbar in O(1) Zeit mit O(n) Aufwand auf einer CREW PRAM. Der Trick ist also das parallele Suchen.
- Erklären Sie die Mediansuche mit linearem Aufwand (sequentiell und parallel)
- Sequentieller Fall
Das k-te Element mit der Eigenschaft 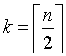 wird durch Unterteilung der Menge S in n/5 Teilblöcke zu je 5 Elementen und Bestimmung des Medians dieser Teilmengen und nachfolgende rekursive Mediansuche auf der Menge der Blockmediane bestimmt. Für den so bestimmten Blockmedian m müssen die folgenden Fälle unterschieden werden. (A und B sind die Teilmengen von S die kleiner oder größer m sind):
wird durch Unterteilung der Menge S in n/5 Teilblöcke zu je 5 Elementen und Bestimmung des Medians dieser Teilmengen und nachfolgende rekursive Mediansuche auf der Menge der Blockmediane bestimmt. Für den so bestimmten Blockmedian m müssen die folgenden Fälle unterschieden werden. (A und B sind die Teilmengen von S die kleiner oder größer m sind):
|A|=k-1: dann ist m bereits das gesuchte k-te Element
|A|>k-1: dann muß man rekursiv das k-te Element von A suchen
|A|<k-1: dann muß man rekursiv das (k-|A|-1)-te Element von B suchen.
Der Zeitbedarf und der Aufwand liegen in O(n).
- Paralleler Fall
Das Problem wird ganz ähnlich wie im sequentiellen Fall gelöst, nur das man jetzt die Folge S in Blöcke der Größe n/logn zu je logn Elementen aufteilt. In jedem der Blöcke wird der Blockmedian bestimmt. Die Blockmediane werden zur Menge M zusammengefaßt. M wird in O(log n) Zeit mit O(n) Aufwand sortiert und man kann den Median m von M sofort ablesen. Man vergleicht parallel jedes Element aus S mit m und erhält wie oben die beiden Mengen A und B und führt die gleiche Fallunterscheidung aus. Damit erhält man: Mediansuche benötigt O(log n log log n) Zeit mit O(n) Aufwand auf einer CREW PRAM.
KE 7 - Konvexe Hülle - Ein parallelisierbares Problem - Grenzen der Parallelisierung
Ist das lineare Optimierungsproblem (LOP) parallelisierbar?
- Rückführung des LOP auf Durchschnitt von Halbräumen
- Einfach parallelisierbar im Fall n=1 (Durchschnitt von Intervallen) und n=2 (Durchschnitt von Halbebenen)
Durchschnitt von Halbebenen
- Duale Transformation auf Problem der konvexen Hülle
- Vorgehensweise zur Bestimmung der konvexen Hülle erläutert
Erklären Sie was ein LOP eigentlich ist!
Wie schnell geht komplexe Hülle und warum geht das so schnell?
Wegen des parallelen Suchens (in O(1) Zeit, Atallah-Goodrich) der richtigen Steigungsintervalle für die Tangente an up(S1), up(S2). Gesamt in O(logn) Zeit mit O(nlogn) Aufwand.
Was versteht man unter den Begriffen konvexe Menge, konvexe Hülle, Halbebene, LOP?
- Konvexe Menge
Eine Teilmenge C der Ebene heißt konvex wenn aus p, q
Î C und a Î [0,1] stets ap + (1-a)q Î C folgt. D.h. gehören zwei Punkte zu C dann gehört auch die Verbindungsstrecke zu C
Konvexe Hülle
Sei S eine Punktmenge. Die konvexe Hülle von S ist definiert durch conv(S)={q | $ k Î N; p1,...,pk Î S; a 1,..., a k Î R: 0≤a i≤1; S ia i = 1; q = S ia ipi}. Also das von der Hüll-Linie - die sich bildet wenn man um eine Punktmenge eine Schlinge zieht - eingeschlossene Gebiet.
Halbebene
Eine Halbebene ist die Menge aller Punkte der Ebene die auf derselben Seite einer festen Geraden l liegen, einschließlich der Punkte von l selbst. Jede Halbebene ist konvex und der Durchschnitt konvexer Mengen ist wieder konvex.
LOP (Lineares Optimierungsproblem)
Ein lineares Optimierungsproblem LOP mit n Variablen x1,...xn besteht aus einer Menge von m linearen Restriktionen
ai1x1+..... ainxn ≤ bi (i=1,...,m)
und einer linearen Zielfunktion
f(x1,....,xn) = a1x1+...+anxn.
Gesucht ist ein Punkt (x1,....,xn), der die Restriktionen einhält und dabei den Wert von f minimiert. Als Spezialfälle wurden die Fälle n=1 (Durchschnitt von Halbgeraden oder Intervallen, lösbar in O(log log m) mit O(m) Aufwand) und n=2 (Durchschnitt von Halbebenen, lösbar in O(log m) Zeit mit O(m log m) Aufwand) diskutiert. Ein allgemeines Lösungsverfahren für n>2 ist der Simplexalgorithmus.
Welches Maschinenmodell ist erforderlich?
Erläutern Sie den Algorithmus von Atallah-Goodrich zur Konstruktion der konvexen Hülle! Welche Grundlagen werden dabei eingesetzt? (par. Suchen und Sortieren!)
Zerlege S in S1={p1,....,p
n/2} und S2=S\S1
Berechne rekursiv und parallel conv(S1) und conv(S2).
Berechne die obere und die untere gemeinsame Tangente an up(S1) und up(S2) bzw. an low(S1) und low(S2).
Ermittle die Geradensteigung aller Streckenstücke p-q in up(S1) und up(S2). Dann läßt sich in O(1) Zeit entscheiden ob f(i)=j, f(i)>j oder f(i)<j ist.
Sei T die obere gemeinsame Tangente, u der erste Punkt von TÇ up(S1) und v der letzte Punkt von TÇ up(S2). Dann setzt sich up(S) aus folgenden Streckenzügen zusammen:
up(S1) von p nach u, T von u nach v,
up(S2) von u nach q.
Berechne analog low(S).
O(log n) Zeit mit O(nlogn) Aufwand auf CREW PRAM.
Wie kann man die parallele Lösung eines LOP mit zwei Variablen auf den Begriff der konvexen Hülle zurückführen?
Ein LOP mit zwei Variablen wird von m linearen Restriktionen beschränkt. Mit anderen Worten: Die Ebene wird von m Geraden in 2m Halbebenen zerschnitten. Die zulässigen Lösungen der Zielfunktion f liegen somit innerhalb der m Ecken des Polygons das durch die Restriktionsgeraden in der Ebene gebildet wird.Das heißt , wenn man den Durchschnitt der m Halbebenen berechnet, erhält man die Ecken des Restriktionspolygons und damit die Lösung des LOP in O(log m) Zeit und O(m log m) Aufwand auf einer CREW PRAM.
Erläutern Sie informell den Begriff der P-Vollständigkeit und seine Bedeutung
Ein Entscheidungsproblem heißt P-vollständig, wenn A
Î P und jedes Entscheidungsproblem BÎ P auf logarithmischem Band reduzierbar auf A ist: BÎ P Î B≤logA
Können Sie einige Beispiele von P-vollständigen Problemen geben?
- Die Berechnung der Ausgabe eines gegebenen aber beliebigen Schaltnetzes für eine Eingabebelegung mit Elementen aus (0,1) ist ein P-vollständiges Problem.
- Berechnung iterierter Restklassen. Eng verwandt damit ist die Berechnung des ggT mit Hilfe des Euklidischen Algorithmus.
- Matching in Graphen (Berechnung derjenigen Kanten die paarweise keine Knoten gemeinsam haben)
![]() .
.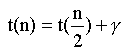 und der Aufwand ist O(n) wegen
und der Aufwand ist O(n) wegen 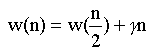
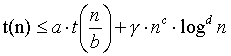
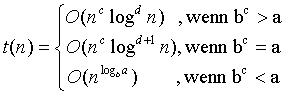 Für t gilt dann folgende Abschätzung:
Für t gilt dann folgende Abschätzung: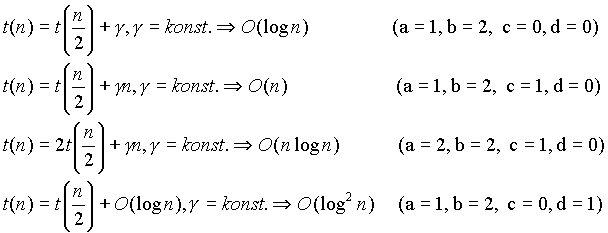
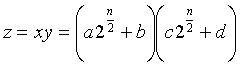
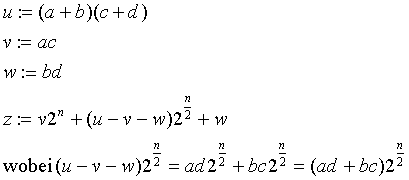
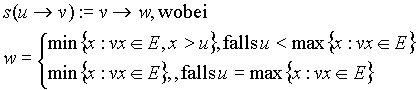
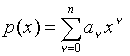 ein Polynom. In Klammerschreibweise erhält man p(x)=a0+x(a1+x(a2+.....+x(an)..)). Löst man diese Klammern von innen nach außen rekursiv auf, erhält man eine lineare Rekurrenz:
ein Polynom. In Klammerschreibweise erhält man p(x)=a0+x(a1+x(a2+.....+x(an)..)). Löst man diese Klammern von innen nach außen rekursiv auf, erhält man eine lineare Rekurrenz: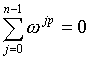
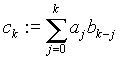 , wobei aj, bj
, wobei aj, bj 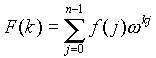 wobei
wobei 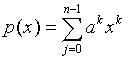 , so gibt Fa offenbar die Werte von p an den Stellen w 0, w 1,....., w n-1 an, denn die i-te Komponente von Fa lautet
, so gibt Fa offenbar die Werte von p an den Stellen w 0, w 1,....., w n-1 an, denn die i-te Komponente von Fa lautet 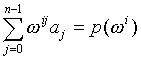 . Ist umgekehrt b der Vektor, der Werte eines Polynoms an den Stellen w i (d.h. bi=p(w i)) dann ist F-1b der Vektor der Koeffizienten von b.
. Ist umgekehrt b der Vektor, der Werte eines Polynoms an den Stellen w i (d.h. bi=p(w i)) dann ist F-1b der Vektor der Koeffizienten von b.
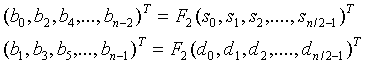
 und
und 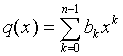 , so gilt (p∙q)(x)=p(x) q(x)=
, so gilt (p∙q)(x)=p(x) q(x)= 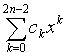 .
.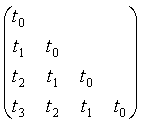
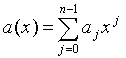 und
und 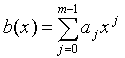 , n>=m mit Hilfe der eindeutig bestimmten Polynome q(x) und r(x) (Quotient und Rest) den Ausdruck a(x)=q(x)b(x)+r(x) bildet. Dabei ist grad(r)<grad(b). Es gilt also q(x)b(x)=a(x)-r(x) und damit wegen der Äquivalenz zwischen Konvolution und Polynommultiplikation
, n>=m mit Hilfe der eindeutig bestimmten Polynome q(x) und r(x) (Quotient und Rest) den Ausdruck a(x)=q(x)b(x)+r(x) bildet. Dabei ist grad(r)<grad(b). Es gilt also q(x)b(x)=a(x)-r(x) und damit wegen der Äquivalenz zwischen Konvolution und Polynommultiplikation 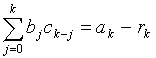 . Für k >= m-1 sind die rk offenbar null und man erhält das Gleichungssystem:
. Für k >= m-1 sind die rk offenbar null und man erhält das Gleichungssystem: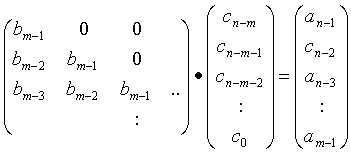
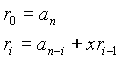 . Benötigt O(logn) Zeit und O(n2) Aufwand.
. Benötigt O(logn) Zeit und O(n2) Aufwand. 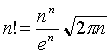 erhält man log2n!=n log n-O(n).
erhält man log2n!=n log n-O(n).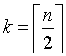 wird durch Unterteilung der Menge S in n/5 Teilblöcke zu je 5 Elementen und Bestimmung des Medians dieser Teilmengen und nachfolgende rekursive Mediansuche auf der Menge der Blockmediane bestimmt. Für den so bestimmten Blockmedian m müssen die folgenden Fälle unterschieden werden. (A und B sind die Teilmengen von S die kleiner oder größer m sind):
wird durch Unterteilung der Menge S in n/5 Teilblöcke zu je 5 Elementen und Bestimmung des Medians dieser Teilmengen und nachfolgende rekursive Mediansuche auf der Menge der Blockmediane bestimmt. Für den so bestimmten Blockmedian m müssen die folgenden Fälle unterschieden werden. (A und B sind die Teilmengen von S die kleiner oder größer m sind):